Wenn Lösungen mit passiven Tilgern nicht möglich sind, muss ein dynamische Schwingungsdämpfer eingesetzt werden. Dieser erfordert naturgemäß eine sorgfältige Beobachtung während des Betriebes und ggf. Wartung.
Er stellt, mechanisch gesehen, eine federnd und dämpfend gelagerte Zusatzmasse dar. Wenn die Zusatzmasse mit der Feder auf die Eigenfrequenz des schwingenden Bauwerks eingestellt werden, geht der Dämpfer bei Schwingung des Hauptsystems in Gegenphase, d.h. Bauwerk und Dämpfermasse schwingen nicht parallel, sondern gegeneinander. Der dabei entstehende Weg wird genutzt, um einen Dämpfer dazwischenzuschalten, der die Energie dissipiert. Bild 9 zeigt die Prinzipskizze am Beispiel eines Stahlkamins:
Bild 9: Anbringung eines Zusatzdämpfers (Prinzip)
Durch das Anbringen der zweiten Masse wird aus dem ursprünglichen Einmassenschwinger (mit der generalisierten Masse M) die ursprüngliche Resonanzspitze in zwei benachbarte Resonanzspitzen aufgespalten. Das Dämpferelement dient dazu, die neuen Resonanzspitzen in ihrer Größe zu beschränken. Wenn das System mit langsam anwachsender Dämpfung berechnet wird, zeigt es sich, dass eine Resonanzspitze weniger gedämpft wird als die andere (Bild 9: Kurve b, c). Die optimale Dämpfung ist offenbar dann erreicht, wenn beide Resonanzspitzen gleich groß werden (Bild 10: Kurve d), vgl. (Petersen, 1996). Wenn die Dämpfung deutlich größer wird als die optimale Dämpfung, blockiert das Dämpferelement immer stärker die schwingende Zusatzmasse, diese wird damit sozusagen starr an das Bauwerk gekoppelt, es entsteht also wieder ein Einmassenschwinger mit der neuen Gesamtmasse M+m (Kurve e,f in Bild 10). Wegen der größeren Gesamtmasse ist die Resonanzspitze leicht nach links gewandert.
Bild 10: Wirkung von unterschiedlich abgestimmten Dämpfern
Die für die optimale Dämpfung erforderlichen Systemabstimmungsparameter nach Den Hartog (Den Hartog, 1952) werden im Folgenden angegeben. Voraussetzung ist eine frequenzkonstant einwirkende Kraftamplitude. M ist die generalisierte Masse des Hauptsystems ohne Dämpfer, m ist die Dämpfermasse. Bei einem Massenverhältnis von
………….(3)
ergibt sich die günstigste Frequenzabstimmung zu
………….(4)
hierin ist f_D die Eigenfrequenz der ungekoppelten Zusatzmasse, f_H ist die ungekoppelte Eigenfrequenz des Haupttragwerkes mit seiner generalisierten Masse. Ungekoppelt soll heißen: Ohne das Zusammenwirken betrachtet. Das optimale Lehrsche Dämpfungsmaß ξ_opt für die Zusatzdämpfung folgt aus:
………….(5)
Das Lehrsche Dämpfungsmaß, auch kritisches Dämpfungsverhältnis genannt, hängt mit dem logarithmischen Dämpfungsdekrement δ wie folgt zusammen: es gilt δ=2 π ξ, vgl. Grundlagen. Der größte Schwingungsausschlag des gedämpften Systems folgt damit zu:
………….(6)
Die angegebenen Formeln gelten für den Fall, dass die einwirkende Kraft frequenzkonstant ist, d.h. sie behält ihre Größe unabhängig von der Frequenz. Bei der Kármánschen Wirbelerregung von kreiszylindrischen Bauwerken trifft dies nicht mehr zu, da die Wirbelablösefrequenz proportional zur Windgeschwindigkeit ist, der Geschwindigkeitsdruck (Staudruck) aber quadratisch mit der Windgeschwindigkeit und damit mit der Frequenz steigt. Das gleiche gilt für Unwuchterregung, die Kraft steigt hier mit dem Quadrat von omega! Die oben angegebenen Formeln gelten dann nicht mehr streng.
Die optimale Frequenzabstimmung bei frequenzquadratischer Anregung ergibt sich zu:
………….(7)
und die optimale Dämpfung zu
………….(8)
Weitere Hinweise hierzu sind in (Sauer 1949 bzw. Wahle 1984) gegeben. Bereits sehr kleine Zusatzmassen (2% bis 5% der generalisierten Tragwerksmasse) führen zu einem starken Anwachsen der effektiven Dämpfung.
Eine Abweichung von der optimalen Dämpfung hat nur einen geringfügigen Einfluss, Abweichungen bei der Frequenzabstimmung haben dagegen starken Einfluss. Ein Dämpfer, der unterhalb seiner Abstimmung betrieben wird, hat praktisch kaum noch eine Wirkung. Ein Betreiben oberhalb der Abstimmung führt zwar zu einer schlechteren Dämpfungswirkung als bei der optimalen Dämpfung, hat aber nicht die drastischen Auswirkungen wie bei einem Betreiben unterhalb der Abspannung. Es empfiehlt sich daher, die Abstimmung vorsichtshalber etwas tiefer als die zu dämpfende Tragwerksfrequenz zu legen, um Ungenauigkeiten abzufangen.
Im Bild 11 sind einige heute eingesetzte Dämpfertypen dargestellt.
Bild 11: Prinzipielle Typen von Dämpfern
Da die technische Realisierung einer sich horizontal bewegenden Masse ziemlich aufwendig ist, wird bei horizontalen Schwingungen gern ein Pendel eingesetzt,. Das Pendel bezieht seine Federsteifigkeit su der Rücktriebskraft der ausgelenkte Masse. Bei kleinen Verformungen sin phi etwa gleich phi, handelt es sich sogar um eine lineare Feder!
Die Federsteifigkeit wird hierbei aus der Rücktriebskraft der Pendelmasse infolge der Erdanziehung gewonnen. Wenn keine Rotation der Zusatzmasse auftritt, gilt für die Eigenfrequenz die des mathematischen Pendels mit der Pendellänge lp:
………….(9)
Die zugehörige Federsteifigkeit für numerische Berechnung des Pendels als federgekoppelte Masse ergibt sich daraus zu:
………….(10)
Wenn Rotationen der Pendelmasse auftreten, kann der Einfluss durch eine sog. reduzierte Pendellänge erfasst werden. Tafeln zur Ermittlung der reduzierten Pendellänge sind in (Klotter, 1955) enthalten. Der Einfluss der Rotationsträgheit kann ausgeschaltet werden, indem eine Masse wie in Bild 12 dargestellt aufgehängt wird. Hierbei rotiert die Masse nicht mehr und die einfache Formel für das mathematische Pendel kann genutzt werden:
.
Bild 12: Pendeldämpfer ohne Rotationsträgheit
Der Verfasser hat auf diese Weise – bei Türmen in der Wüste – Dämpfer unter die Kanzeln von stark schwingenden Beobachtungstürmen ausgeführt, in dem eine Sandkiste an vier Seilen unter dem Kabinenboden abgehängt und mit Sand gefüllt wurde (davon gab es ausreichend). Unter dem Kabinenboden wurde dann ein Stab als vertikaler Kragarm angebracht, der in den Sand der Kiste hineinragte. Die Kiste schwang dabei also um den „Rührstab“ herum und nicht – wie üblich – umgekehrt. Die Eintauchtiefe wurde so angepasst, dass die Schwingungen verschwanden. Damit war die optimale Dämpfung zumindest näherungsweise erreicht.
Bei nicht zu großen notwendigen Dämpfungswerten werden heute sehr gern sog. Flüssigkeitsdämpfer eingesetzt. Eine Flüssigkeitsmenge in einem rechteckigen oder runden Behälter wird mit einer (vorzugsweise nicht gefrierenden) Flüssigkeit so weit befüllt, bis die Schwappfrequenz gleich der Bauwerkseigenfrequenz ist. Diese hängt ab von der Beckenform und der Wassertiefe. Die beim Schwappen entstehende Anprallkraft wirkt in Gegenphase und deshalb wie eine Dämpfung. Siehe Abschnitt Flüssigkeitsdämpfer.
Diese Form entspricht zunächst direkt dem mechanischen Modell. Die Masse wird über mechanische Federn an die schwingende Struktur angekoppelt. In Bild 1 ist das Prinzip dargestellt. Der Dämpfer wirkt gegen eine vertikale Schwingung. Die Masse ist über die Federn gelagert, im Zentrum oder in der Symmetrielinie sind Dämpfer angebarcht. Diese funktionieren meist nach dem Prinzip „Hingtopf“. Eine zähe, viskose Masse im Topf wird durch den Stempel, der an den schwingenden Massen befestigt ist, „durchgewalkt“. Dabei wird Energie vernichtet. Die Federn und das Dämpfungsmaß werden nach den Formeln im Hauptkapitel passive Dämpfer bemessen.
Bild 1: veertikal wirkender Dämpfer
Man erkennt seitlich zwei Führungen, die die Massenbewegung in eine vertikale Richtung erzwingen. Solche Dämpfer können mit einer sehr geringen Bauhöhe realisiert werden, so dass sie auch in sehr schlanken Fußgängerbrücken eingesetzt werden können und eingesetzt werden. Für größere Brücken müssen die schwingenden Dämpfermasser natürlich größer werden, Das Massenverhältnis ist ein wesentlicher, steuernder Parameter der Dämpferbemssung, vgl passive Dämpfer. Bild 2 zeigt einen größeren Dämpfer für eine Schrägseilbrücke. Dere Dämpfer stammt von der Fa. Maurer, München, die eine große Zahl von Dämpfern unterschiedlicher Ausbildung im Programm hat und dabei auch das zugehörige Engineering mit erledigt.
Bild 2: Feder-Dämpfer der Fa.Maurer, München
Wenn zusätzlich zur vertikalen Bewegungsrichtung auch die horiziontale mit bedämpft werden soll, müsse auch horizontale Federn eingesetzt werden. Die Führung entfällt dabei naturgemäß. Da auch die vertikalen Federn eine Quersteifigkeit haben, muss dieser Effekt bei der Dimensionierung der horizontalen Federn berücksichtigt werden. In Bild 3 ist eine Prinzipskizze eines vertikal und horizontal wirkenden Dämpfers dargestellt. Bei reiner Horizontaldämpfung und ggf. großen Dämpfermassen kann überlegt werden, die vertikalen Federn durch eine Kugelauflagerung zu ersetzen, so dass der Dämpfer sich in Querrichtung frei bewegen kann. Natürlich muss dann für das Dämpferelement eine andere Lösung gefunden werden als in BIld 3. Denkbar wäre z.B. eine kreisförmige Aussparung in der Masse, die dann mit einem visoelastischen Material, wie z.B. Neopren gefüllt wird. Auf der Grundplatte wird ein Stempel vorgesehen, der voll in das Neopren eingreift (Bild 4).
Bild 3: Dämpfer mit vertikaler und horizontaler Wirkung
Das Bedämpfen der horizontalen Richtung ist bei Fußgängerbrücken wichtig, da beim Gehen stets auch neben der vertikalen periodischen Erregung durch die auftretenden Füße, ein e horizontale Errgung stattfindet, da die Beine in einem leichten Winkel seitlich stehen udn somit beim Auftreten auch eine geringe Komponente in Querrichtung hervorrufen. Die Periode der Quererregung ist halb so groß, wie die der vertikalen Erregung. Die Frequenz entspricht also der halben Schrittfrequenz. Hierduch werden Schwingungen sehr geringer Frequenz angeregt, die aber, wenn sie in Resonanz erfolgen, erhebliche Querschwingungen zur Folge haben können.
Bild 4: Dämpfer mit rein horizontaler Wirkung und Kugellagerung
Es sei darauf hingewiesen, dass alle Elemente des Dämpfers dauerfest konstruiert werden müsse, da sonst Ermüdungsbrüche zu erwarten sind.
Den Hartog, J.P. (1952): Mechanische Schwingungen. Berlin, Göttingen, Heidelberg: Springer 1952.
Klotter,K. (1955):Schwingungen. In: Hütte, Des Ingenieurs Taschenbuch. Berlin: W. Ernst&Sohn.
Peil,U. (1993): Baudynamik. In: Stahhlbau Handbuch,Band I Teil A. Stahlbau-Verlagsgesellschaft mbH, Köln.
Petersen,C. (1996): Dynamik der Baukonstruktionen. Friedr. Vieweg&Sohn, Braun-schweig, Wiesbaden, 1996.
Petersen,C. (2001): Schwingungsdämpfer im Ingenieurbau. Herausgeber: Firma Mauer und Söhne, GmbH und Co KG, München.
Pritchard, B.P.: The use of shock transmission units in bridging. Proc,. Instn. Civ. Engrs. Structs&Bldgs, 1996,116, p.82-95. Sauer,F.M., C.F.Garland (1949): Performance of the Viscously Damped Vibration Absorber to Systems having Frequency Squared Exitation. Journ. of Appl. Mech. 16,109-117
Wahle,M.(1984): Beitrag zur passiven Kontrolle schwach gedämpfter elastischer Strukturen mittels dynamischer Schwingungsdämpfer. Dissertation RWTH Aa-chen, 1984. Kurino,H., J. Tagami, K.Shimizu,T.Kobori: Switching Oil Damper with built in controllere for structural control. Journ. of Struct. Eng, AASCE, Juky 2003, p.895-304.
Da die technische Realisierung einer sich horizontal bewegenden Masse ziemlich aufwendig ist, wird bei horizontalen Schwingungen gern ein Pendel eingesetzt,. Das Pendel bezieht seine Federsteifigkeit su der Rücktriebskraft der ausgelenkte Masse. Bei kleinen Verformungen sin phi etwa gleich phi, handelt es sich sogar um eine lineare Feder!
Die Federsteifigkeit wird hierbei aus der Rücktriebskraft der Pendelmasse infolge der Erdanziehung gewonnen. Wenn keine Rotation der Zusatzmasse auftritt, gilt für die Eigenfrequenz die des mathematischen Pendels mit der Pendellänge lp:
………….(1)
Die FOrmel gilt nur für den Fall, dass die Rotations-Trägheit der bewegten Masse vernachlässigt werden kann. Man spricht dann vom sog. Mathematischen Pendel, also einem idealisierten Pendel, das in der physikalischen Wirklichkeit nicht ausgeführtr werden kann, da jede Masse eine gewisse Ausdehmumg hat. Die Annahme verschwindender Rotations-Massenträgheit kann deshalb auch nur näherungsweise getroffen werden, wenn die Ausdehnung der Masse klein ist. Bei größeren Massen wirkt die Rotations-Massenträgheit deutlich mit (Physikalisches Pendel) und muss berücksichtigt werden. Dies kann (ohne Ableitung) durch eine Korrektur der Pendellänge erfolgen. Man spricht von einer reduzierten Pendellänge, obwohl es sich i.d.R. eine Vergrößerung der Pendellänge handelt. Bessere wäre Ersatzpendellänge. Die zusätzliche Rotationsmassenträgheit vergrößert ja die Massenträgheit, damit sinkt die Frequenz (siehe Gl. 2), dies kann deshalb nur durch eine größere Pendellänge erfasst werden. Es gilt:
………………(2)
Der Index 0 bei J bedeutet, dass das Rotatiosns-Massenträgheitsmoment auf den Drehpunkt des Pendels bezogen ist. Für das Rotations-Massenträgsheitsmoment wird hier der Buchstabe J verwendet, im Gegensatz zum I für das Querschnittsflächenträgheitsmoment. Mit der so ermittelten Ersatzpendellänge l_red kann dann, wie beim Mathematischen Pendel gearbeitet werden. Bild 1 zeigt das zugrunde liegende System eines nicht mathematischen – also physikalischesnPendels – mit der Gesamtmasse m_ges und Schwerpunktsabstand e vom Drehpunkt.
Bild 1: Physikalisches Pendel mit Rotationsmassenträgheit
Das Rotationsmassenträgheitsmoment J_0 ergibt sich bekanntlich zu:
………………(3)
Die Formel entspricht also völlig dem bekannten Ansatz für das Querschnittsflächen-Trägheitsmoment I, mit dem Unterschied, dass dort nach einem Flächenelement dF integriert wird, hier dagegen nach einem Massenelement dm. Da aber die Masse nichts weiter ist als die Fläche mal Dichte mal Dicke der Fläche, ändern sich nur die Vorfaktoren. Es kann somit auch geschrieben werden:
………………(4)
Wenn der Schwerpunkt noch nicht bekannt ist, kann zunächst ein beliebiger Bezugspunkt gewählt werden, das sich so ergebende Massenträgheitsmoment muss dann noch um den Steiner-Anteil korrigiert werden. ganz so wie man es von der Berechnung von Flächen-Querschnittswerten her kennt:
………………(5)
Die Koordinaten mit dem Index S sind die Abstände von der beliebigen Bezugsachse zum Schwerpunkt.
Quadratischen Querschnitt mit konstanter Dicke t (Bild 2)
Bild 2: Rechteckquerschnitt konstanter Dicke t
Daraus ergibt sich:
………………(6)
Tafeln zur Ermittlung der reduzierten Pendellänge sind in (Klotter, 1955) enthalten. In Petersen (1996) sind im Kap. 4.7 auch für Pendel mit Zusatzfedern Formeln abgeleitet!
 |
Da Pendel oft eingesetzt werden, wenn Schwingungen in alle Richtungen auftreten können, wird hierfür meist eine zylindrische Masse an einem zylindrischen Stab verwendet, so dass in allen Richtungen die gleichen Bedingungen herrschen. Für diesen – praktisch häufig vorkommenden – Fall sollen noch die Formel für das Rotations-Massenträgheitsmoment angegeben werden, siehe dazu auch Petersen (1996), Abs. 4.7.4: |
Da Pendel oft eingesetzt werden, wenn Schwingungen in alle Richtungen auftreten können, wird hierfür meist eine zylindrische Masse an einem zylindrischen Stab verwendet, so dass in allen Richtungen die gleichen Bedingungen herrschen. Für diesen – praktisch häufig vorkommenden – Fall sollen noch die Formel für das Rotations-Massenträgheitsmoment angegeben werden, siehe dazu auch Petersen (1996), Abs. 4.7.4:
Bild 3: Zylindrisches Pendel als Beispiel
Die Massen ergeben sich wie folgt:
…………….. (7)
Die Massenträgheitsmomente bezüglich ihrer bekannten Einzelteil-Schwerpunkte sind:
……………. (8)
Bezogen auf den Aufhängepunkt ergibt sich incl. der Steiner Anteile:
. ……………..(9)
Damit ergibt sich die Lage des Gesamtschwerpunktes zu:
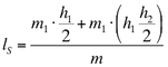. ……………..(10)
Falls für Berechnungen mit einer federgekoppelten Masse die zugehörige Federsteifigkeit des Pendels benötigt wird, ergibt sich diese zu:
………….(11)
In einem Physikalischen Pendel treten Schnittkräfdte N,M,Q auf. Diese können einfach, unter Anwendung des Schnittprinzips ermittelt werde, wobei man zweckmäßig am freien Rand beginnt, denn dort sind alle SChnittkräfte gleich Null. Die Schnittkräfte sind wichtig für den Ermüdungsnachweis des Pendels!
Der Einfluss der Rotationsträgheit kann ausgeschaltet werden, indem eine Masse wie in Bild 4 dargestellt aufgehängt wird. Hierbei rotiert die Masse nicht mehr und die einfache Gl.(1) für das mathematische Pendel kann genutzt werden:
.
Bild 4: Pendeldämpfer ohne Rotationsträgheit
Der Verfasser hat auf diese Weise (mit der Parallelogrammkonstruktion) – bei Türmen in der Wüste – mit „Bordmitteln“ Dämpfer unter der Kanzeln stark schwingender Beobachtungstürme ausgeführt, in dem eine Sandkiste an vier Seilen, mit zur Frequenz passender Länge l_P, unter dem Kabinenboden abgehängt und mit Sand gefüllt wurde (davon gab es ausreichend). Unter dem Kabinenboden wurde dann ein Stab als vertikaler Kragarm angebracht, der in den Sand der Kiste hineinragte. Die Kiste schwang dabei also um den „Rührstab“ herum und nicht – wie üblich – umgekehrt. Die Eintauchtiefe wurde so angepasst, dass die Schwingungen verschwanden. Damit war die optimale Dämpfung zumindest näherungsweise erreicht.
Petersen, C.: Dynamik der Baukonstruktionen. FR. Vieweg & Sohn Verlag, Braunschweig, Wiesbaden, 1996.
Klotter, K.: Technische SchwingungslehreI. 2. Auflage, bBerlin, Göttingen, Heidelberg, Springer, 1960.
Peil,U.: Baudynamik. In Stahlbau-Handbuch 1A, Stahlbauverlagsgesellschaft, Köln, 1993.
Peil,U.: Baudynamik für die Praxis. In: Stahlbau-Kalender 2008, Hrgb. U. Kuhlmann, Ernst&Sohn, Berlin, 2008, p.390-476.
Den Hartog, J.P. (1952): Mechanische Schwingungen. Berlin, Göttingen, Heidelberg: Springer 1952.
Klotter,K. (1955):Schwingungen. In: Hütte, Des Ingenieurs Taschenbuch. Berlin: W. Ernst&Sohn.
Petersen,C. (2001): Schwingungsdämpfer im Ingenieurbau. Herausgeber: Firma Mauer und Söhne, GmbH und Co KG, München.
Pritchard, B.P.: The use of shock transmission units in bridging. Proc,. Instn. Civ. Engrs. Structs&Bldgs, 1996,116, p.82-95. Sauer,F.M., C.F.Garland (1949): Performance of the Viscously Damped Vibration Absorber to Systems having Frequency Squared Exitation. Journ. of Appl. Mech. 16,109-117
Wahle,M.(1984): Beitrag zur passiven Kontrolle schwach gedämpfter elastischer Strukturen mittels dynamischer Schwingungsdämpfer. Dissertation RWTH Aa-chen, 1984.
Wenn die Kugel auf einer Kreisbahn läuft, besteht eine unmittelbare Analogie zum Pendeldämpfer, bei dem sich die Kugel ebenfalls auf einer Kreisbahn bewegt. Der wesentliche Unterschied ist der, dass die rollende Kugel ein beträchtliches Rotations-Trägheitsmoment aufweist, da sie sich mehrfach abrollen kann. Die Rotationsträgheit zehrt ein Teil der Kraftwirkungen auf. Beim Pendel ist der Pendelwinkel meist sehr gering, so dass die zu berücksichtigende Rotation klein bleibt. Beim Pendel mit Parallelogramm-Abhängung bleibt dieser Anteil komplett Null.
Sowohl das Pendel ohne Dämpfer als auch die reine Kugel sind im Grunde Tilger, da hier keine Energie dissipiert wird, sondern Gegenkräfte zur Strukturbewegung generiert werden. Die grundlegenden Bezeichnungen werden in Bild 1 erläutert.
Bild 1: Definitionen und Bezeichnungen
Die Gleichgewichtsbedingungen ergeben sich durch Zusammenfassung der äußeren Kräfte und der d’Alembertschen Trägheitskräfte:
…………………(1)
Mit den Geometriebedingungen
, ………………(2)
Durch Zudsammenfssung ergibt sich die Bewegungsdifferentialgleichung. Diese wird wie in den Grundlagen, Kap. 3.1. gelöst. Daraus ergibt sich wie in den Grundlagen Kap. 3.1. die Eigenfrequenz f:
………………. (3)
Der Index K bezieht sich hier auf die Kugel. a ist in den Formeln die Beschleunigung (acceleration) des Kugelschwerpunktes, g die Erdbeschleunigung.
Man erkennt, dass ein großes Rotations-Trägheitsmoment die Eigenfrequenz absenkt. Bei konstant gehaltener Masse m_K steigt daas Rotations-Massenträgheitsmoment und sinkt entsprechend die Eigenfrequenz, wenn immer mehr Masse nach außen gebracht wird, Es sollen 3 Fälle betrachtet werden. Darin ist J_K das Rotations-Massenträgheitsmoment bezüglich des Kugel-Schwerpunktes, J_0 ist bezogen auf den oberen Drehpunkt 0. Die Eigenfrequenz f ist in Hertz angegeben [Hz]. In der letzten Spalte ist die Geometrie angegeben, die erforderlich sit, um eine vorgegebene Frequenz f zu erreichen.
Tabelle 1: Formeln für unterschiedliche Massenbelegung der Kugel
Man erkennt, dass die Rotationsmasse der Kugel die Eigenfrequenz senkt, wie es zu erwarten ist. Je größer der Anteil der Masse ganz außen ist, desto größer wird das Rotations-Massenträgheitsmoment. Vgl. dazu das bekannte Querschnittsflächen-Trägheitsmoment. Auch dies wird maximal, wenn die Fläche möglichst weit außen plaziert wird. Aus diesem Grunde ist die Hohlkugel der ungpünstigste Fall, da hier die gesamte Masse außen sitzt. Natürlich ist, wie im Fall der hohlen Kugel (b.) eine Masse der Schale bei einer Dicke t=0 unmöglich. Dies ist eine idealisierende Annahme, die die Berechnung etwas erleichtert.
Die Dämpfungswirkung entsteht durch die phasenverschobene Gegenkraft, die durch die Kugen auf die Rollbahn abgesetzt wird: Schwingt das Bauwerk nach links, rollt die Kugel in Gegenphase nach rechts und übt dort Kräfte auf die Rollbahn aus, die der Bewegung entgegengesetzt sind. Dadurch wird die Bauwerksbewegung gedämpft.
Für die rückstellende Kraft der auf der Kreisbahn rollenden Kugel ergibt sich, bei Voraussetzung kleiner Verformungen:
. …………….. (4).
Die Kräfte T und H ergeben sich aus den d’Alembertschen Gleichgewichtsbedingungen:
Mit
………………… (5)
und
………………. (6)
ergibt sich dann:
………………….(7)
und
. …………… (8)
Der reine Pendeldämpfer erzeugt eine Rückstellkraft der Größe:
…………….. (9).
Man erkennt, dass die Einflüsse aus dem Rotationsträgheit der rollenden Kugel auch die Rückstellkraft reduzieren, die Dämpfungswirkung also geringer wird, als beim vergleichbaren Pendel gleicher Masse und passender Pendellänge. Diese Schlechterstellung ist bedingt durch den Effekt der Rotationsträgheit, die dazu führt, dass die Kontaktkräfte der rollenden Kugel durch die Rotationsträgheit reduziert wird. Die Formeln (7) und (8) zeigen, dass durch das letzte Glied, bei dem J_0 im Nenner steht, die Kräfte abgemindert werden.
Im Folgenden werden die drei untersuchten Fälle a,b,c nach Tabelle 1 in ihrer Effizienz mit dem Pendeldämpfer verglichen:
Tabelle 2: Vergleich mit einfachem Pendel
Wenn der Kugeldämpfer die gleiche Dämpfungswirkung wie ein analoges Pendel haben soll, muss die Kugelmasse mit den Kehrwerten der Effizienzwerte aus Tabelle 2 vergrößert werden. Leider steigt hierdurch i.a. auch der Radius, so das ein Teil des Effektes aufgezehrt wird.
In [1] wird über Versuche berichtet, die mit einem Kugeldämpfer durchgeführtr wurden., Dieser wurde dazu an der Spitze eines Kragarms montiert. Die Dämpfung wurde nach Anzupfen durch Messung der Amplitudenabnahme bestimmt, vgl. Grundlagen. In Bild 2 sind die Ergebnisse dargestellt. Achtung: Das Massenverhältnis (im Bild gamma, in den Dämpfergrundlagen mue, ist auf der Ordinate eingetragen!
Interessant ist auch, dass die Dämpfungswirkung steigt, wenn man mehrere Kugeln einsetzt (coupled motions), die in der Summe die gleiche Masse haben, wie die eine Vergleichskugel. Dies leuchtet auch unmittelbar eiin. Die einzelnen Kugeln haben dann naturgemäß einen geringeren Durchmesser. Wegen der quadratischen Abhängigkeit des Rotations-Massenträgheitsmomentes vom Radius wird die Gesamt Rotatiosnträghgeit geringer, die Effizienz des Dämpfers steigt also. Außerdem treten zusätzliche Reibungen und Impulsübertragung zwischen den Kugeln auf, was ebenfalls die Dämpfunsgwirkung verbessert. In Bild 2 sind die Ergebnisse dargestellt:
Bild 2: Logarithmisches Dekrement delta über dem Massenverhältnis mue.
Bild 3 zeigt die Geometrie des Dämpfers. Man erkennt den relativ geringen Unterschied der Radien. Dieser liegt bei (410-300)=110mm=0,11 m. Daraus lässt sich die zugehörige Eigenfrequenz bestimmen. Tabelle 1 entnimmt man die Geometrie aus der 1 Zeile, letzte Spalte. Es gilt:
…………. (10)
Aufgelöst nach f folgt: 
. ……………..(11)
Bild 3: Geometrie des verwendeten Dämpfers
Dämpfungsmessungen am konkreten Bauwerk (Gitterturm) zeigten sehr gute Dämpfungswerte. Die gemessenen Reaktionen konnten um etwa 14 bis 40% reduziert werden. Der Dämpfer hat so, wie beschrieben, kaum innere Dämpfung, Der Verfasser ist derzeit dabei, durch eine einfache Modifikation zusätzliche Dämpfung, ggf. auch nichtlinear, zu generieren.
Wie kann ein sog. Kugeldämpfer iun einem Rechenmodell erfasst werden?
Die Antwort ist einfach: Als ganz normale Masse, die an die Hauptstruktur angelenkt ist (Bild 4).
Bild 4: Modelle eines Kugeldämpfers
(siehe dazu Begründung unterhalb dieser Aufzählung).Begründung für die Formel zur Steifigkeit k: Die Kreisfrequenz des angefederten Einmassenschwingers soll gleich der Kreisfrequenz dee Kugel, vgl. Gl (3), sein:
oder mit Nutzung der zusammengefassten Formeln in der letzten Spalte von Tabelle 1:
Vollkugel: 
.
Für die anderen Fälle sind die Faktoren entsprechend anzupassen.
Das entspricht im Prinzip der Formel für das Pendel: 
mit korrigierter Pendellänge.
[1] Pirner,M., O. Fischer: The developement of a ball vibration absorber for the use on towers. In: Jour n. Int. Assoc. for Shell and Spatial Struct. Vol. 41, No.2 , 2000p 91-100.
Peil,U. (1993): Baudynamik. In: Stahhlbau Handbuch,Band I Teil A. Stahlbau-Verlagsgesellschaft mbH, Köln.
Petersen,C. (1996): Dynamik der Baukonstruktionen. Friedr. Vieweg&Sohn, Braun-schweig, Wiesbaden, 1996.
Petersen,C. (2001): Schwingungsdämpfer im Ingenieurbau. Herausgeber: Firma Mauer und Söhne, GmbH und Co KG, München.
Sauer,F.M., C.F.Garland (1949): Performance of the Viscously Damped Vibration Absorber to Systems having Frequency Squared Exitation. Journ. of Appl. Mech. 16,109-117
Wahle,M.(1984): Beitrag zur passiven Kontrolle schwach gedämpfter elastischer Strukturen mittels dynamischer Schwingungsdämpfer. Dissertation RWTH Aa-chen, 1984.
Ein völlig anderes Dämpferprinzip stellen die sog. Anschlagdämpfer dar, im Englischen als bumper-damper bezeichnet. Hierbei wird entweder ein Pendel abgehängt, das nicht über zusätzliche, ständig dämpfende Elemente verfügt (Bild 1). Das Pendel schlägt an den Rand und erzeugt damit einen Impuls mit einer Kraft die der Bewegung entgegengesetzt ist und deshalb eine dämpfende Wirkung hat (Bild 1).
Da das Abhängen eines schweren Pendels oft mit erheblichem konstruktiven Aufwand verbunden ist, kann die Lösung auch durch eine z.B. parabel- oder kugelförmig ansteigende (ggf. räumliche) Rollbahn erreicht werden (Bild 2). Allerdings sind hier die ungünstige Wirkung der Rotationsträgheit zu beachten, vgl. Kap Kugeldämpfer.
 |
 |
| Bild 1: Anschlag-Pendeldämpfer … | Bild 2: Anschlag-Kugeldämpfer |
| . |
Die Formeln für die Eigenfrequenzen und Dämpfungswirkung der rollenden Kugel sind den beiden Unterkapiteln Pendeldämpfer bzw. Kugeldämpfer zu entnehmen.
Der Anschlag am Ende kann mit HIlfe eines Stoßdämpfers, bzw. Ringfeder-Elementes oder Shock-Absorber (je nach Kraft) ausgebildet werden, dann wird zusätzlich zur rückstellenden Kraft des sich etwa in Gegenphase bewegenden Pendels (oder Kugel) noch etwas Dissipation aktiviert. Außerdem sind die lokalen Beanspruchungen kleiner, was naturgemäß ermüdungsmäßig günstig ist. In Bild 3 wird das noch einmal deutlich. klein-omega ist hierbei die Eigenfrequenz des (Pendel)Dämpfers, Groß-omega die Frequenz der Systemerregung, also die zu bedämpfende Systemfrequenz. Wenn Groß-omega/Klein-omega kleiner ist als 1, befinden wir uns rechts von der Resonanzfrequenz.
Bild 3: Vergrößerungsfunktion in Abhängigkeit des Frequenzverhältnisses
Ein Beispiel für einen Anschlag (Bumper) Dämpfer ist das sog,. System Fette, vgl. Bild 4. Die Ringmasse ist an Pendeln abgehängt und schlägt gegen Kunststoff-Anschlagdämpfer.
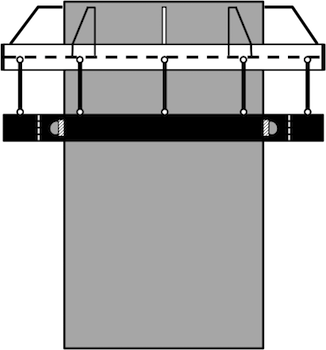
Bild 4: Bumper Dämpfer mit abgehängter Ringmasse (System Fette)
Die Pendellänge ist so gewählt, dass die Eigenfrequenz des Anschlagpendels deutlich unter der des schwingenden Systems liegt. Der Dämpfer ist also tief abgestimmt, gegen das System, so dass er bei Fußpunkterregung durch das System kaum noch Bewegungen zeigt, vgl. Grundlagen.Abstimmung. Das Video in den Grundlagen macht das sehr deutlich: Die den Fußpunkt des Schwingers (Kugel am Gummiband) erregende Hand entspricht dem System, die Kugel der Dämpfermasse. Man erkennt, wie bei niedriger Erregerfrequenz, d.h. wenn die (Hand)Erregerfrequenz geringer ist als die Frequenz der (Dämpfer)Masse, die Masse etwa der Fußpunktbewegung folgt. Die Masse ist also noch in Phase, sie bewegt sich parallel wie die Struktur (die Hand). Ein Anstoßen kann deshalb nicht stattfinden. Wenn dagegen die Handerreger (System)frequenz größer ist als die Eigenfrequenz der Masse, befindet sich die Masse in Gegenphase und kommt bei hohen Erregerfrequenzen praktisch zum Stehen. In diesem Frequenzbereich können also Anschläge stattfinden, wenn die Freiräume der Masse geringer sind als die Schwingbewegung.
Die Eigenfrequenz eines mathematischen Pendels ergibt sich zu:
Daraus ergibt sich die erforderliche Länge, wenn eine Frequenz f bedämpft werden soll:
Es empfiehlt sich, die Länge zur Abfangung von Unsicherheiten bei der Systembildung um einen Faktor > 1,25^2 etwa 1,5 zu vergrößern. Da die Länge unter der Wurzel steht, entspricht dies einer Frequenzverkleinerung von etwa 1,25. Damit ist der Resonanzbereich weit genug entfernt, vgl. Bild 2. Das bedeutet, dass die Pendellänge bei einem Schornstein, bei dem die wichtige unterste Eigenfrequenzen f_1=1,1 Hz beträgt, eine Länge von mindestens:
aufweisen sollte.
Bei Schwingungen des Schornsteins bleibt die Masse des abgehängten Ringes wegen ihrer Trägheit etwa in Ruhe. Der Schornstein schlägt also regelmäßig an die äußere Ringmasse, wodurch Gegenkräfte geweckt werden, was einen erheblichen Dämpfungseffekt hat.
Zur Berechnung der Anschlagkräfte: Der Impulssatz fordert, dass die Änderung des Impulses gleich dem entstehenden Kraftstoß ist (v und F sind Vektoren, also gerichtete Größen, mit Überstrich-Pfeil gekennzeichnet):
……………….. (1)
Daraus folgt die Kraftamplitude:
. …………………(2)
Je nach Federgesetz des Anschlags ergeben sich unterschiedliche Kräfte oder Eindrückungen. Für das Federgesetz wird die folgende Annahme getroffen (Bild 3). Wenn F_0 = 0 ist ist es eine reine Feder mit der Steifigkeit C. Wenn F_0 größer wird, wird zunächst ohne Eindrückung reagiert, bis sich dann bei wachsender Kraft eine Verschiebung einstellt.
Bild 5: Federgesetz des Anschlages
Die Formel (2) muss nach der gesuchten Größe aufgelöst werden. Wenn man von einer reinen Feder ausgeht (F_0=0, C>0) ergibt sich z.B. für den Eindrückweg und die Kraft: 
. …………………(3)
Wenn der Anschlag am Umkehrpunkt der Pendelschwingung angebracht wird, ist er wirkungslos, da die Geschwindigkeit dort Null ist. Dies wird durch eine kurze Pendellänge erreicht.
Klotter,K. (1955):Schwingungen. In: Hütte, Des Ingenieurs Taschenbuch. Berlin: W. Ernst&Sohn.
Peil,U. (1993): Baudynamik. In: Stahhlbau Handbuch,Band I Teil A. Stahlbau-Verlagsgesellschaft mbH, Köln.
Petersen,C. (1996): Dynamik der Baukonstruktionen. Friedr. Vieweg&Sohn, Braun-schweig, Wiesbaden, 1996.
Petersen,C. (2001): Schwingungsdämpfer im Ingenieurbau. Herausgeber: Firma Mauer und Söhne, GmbH und Co KG, München.
Sog. Schockabsorber sind im Grunde einem normalen hydraulischen Dämpfer sehr ähnlich. Der wesentliche Unterschied besteht in der Art der Füllung des Zylinders, Bei Schockabsorbern ist dieser Raum z.B. mit einem zähplastischen Silikon oder einem Neopren gefüllt. Beide Stoffe sind unter hohem Druck plastizierfähig. Bei einer Kolbenbewegung drängen sie i.a. seitlich am Kolben, d.h. zwischen Kolben und Zylinderwand durch. Dabei wird sehr viel Arbeit vernichtet. Schockabsorber werden deshalb mit Vorzug dort eingesetzt, wo große Kräfte wirken.
Schock-Absorber dienen der Dämpfung sehr hoher Kräfte, die gelegentlich dynamisch auftreten können. Im Regelfall handelt es sich bei den Schock-Absorbern um Konstruktionen, die hydraulischen Dämpfern ähneln. Der Kolbendurchmesser hat ein planmäßiges Untermaß, verglichen mit dem lichten Zylinderdurchmesser. Durch diese Lücke bewegt sich das Silikon oder eine andere Füllung, wenn der Kolben bewegt wird. Hierbei werden große Arbeitsbeträge vernichtet.Bei sehr großen Kräften wird als Füllmaterial gelegentlich auch Neopren eingesetzt, das ebenfalls viscoplastisches Verhalten zeigt. Dabei wird sehr viel Energie vernichtet. Bild 1 zeigt eine Prinzipskizze. Man erkennt, dass der Absorber mit einem Silikon gefüllt ist und nicht, wie bei Stoßdämpfern sonst üblich, mit Öl.
Bild 1: Schock-Absorber
In Bild 2 ist das typische Verhalten solcher Schock-Absorber dargestellt [Pritchard, 1996].
Leider sind die einwirkenden Kräfte in der Literaturstelle nicht in kN angegeben, sondern in t, d.h. Tonnen. Da alle Literaturziate aus dem britischen Bereich stammen, kann man annehmen, dass es sich um britische Tonnen tn handelt. Hierfür gilt die Umrechnung 1 t = 0,984 tn. In guter Näherung kann der kleine Unterschied im Rahmen der im Bauwesen üblichen Genauigkeit vernachlässigt werden, d.h. 1 t entspricht 10kN.
Schock-Absorber werden erfolgreich eingesetzt, um z.B. Brückenüberbauten an den Pfeilerköpfen so zu befestigen, dass ein großer Teil der dynamischen Energien (z.B. aus Erdbeben) vernichtet wird. Die folgende Tabelle 1 zeigt einige Haupt-Charakteristika von Schock-Absorbern.
Bild 2; Zyklischer Test einer Schock-Absorber Einheit
Diese Diagramm mag als Hilfe für die Vorbemessung auch bei anderen Parametern dienen. Extrapolationen in nicht zu großen Entfernungen scheinen in Anbetracht des relativ regulären Verhaltens erlaubt. Bei Extrapolationen in entferntere Parameterbereiche sind jedoch Eignungs-Versuche erforderlich. Größere Kräfte auch durch Parallelschaltung mehrerer bekannter Einheiten übertragen werden. Zur ersten Orientierung möge die Tabelle 1 dienen, die einige wesentlcihe Parameter enthält.
Tabelle 1: Charakteristika ausgewählter Schock-Absorber
Wenn größere Kräfte übertragen werden müssen, können, wie erwähnt, die o.a. Elemente durch Parallelschaltung leicht dazuherangezogen werden. Solche Schock-Absorber haben eine viskoelastisch-plastisches Verhalten, d.h. sie wirken geschwindigkeitsabhängig. Bei sehr langsamen Änderungen kriecht der Schock-Absorber relativ kraftfrei in eine neue Position. Bei sehr rasch einwirkenden Kräften überträgt er einen Großteil der Kraft. Solche System sind eingesetzt worden, um die horizontalen Erdbebenkräfte bei hoher Dämpfung in mehrere Pfeiler zu übertragen und gleichzeitig eine weitgehend kraftfreie Aufnahme sehr langsamer Temperatur-Wegänderungen zu gewährleisten und somit die Pfeiler von dieser hohen Zwangsbeanspruchung zu entlasten, siehe Bild 3.
Bild 3: Schock-Absorber bei einer Brücke im Erdbebengebiet
Ein anderer Typ von Shock Absorbern ist die sog. Ringfeder, die von der gleichnamigen Firma vertrieben wird.
Die bei der Stauchung erzeugte Ringdehnung ist elastisch. Durch die Ringdehnung und die dadurch verursachten Rutschungen wird über die aktivierte Reibung zwischen den Ringflächen Energie in hohem Maße dissipiert. Die Elemente können vorgespannt werden, so dass auch ein Einsatz bei Zugbeanspruchung möglich ist. Der Verfasser hat mit solchen Elementen schwere Innenliner (Rauchgasrohre in Stahlbetonschornsteinen) gedämpft. In Bild 4 ist eine solche (graphisch) aufgeschnittene Feder zu sehen. Die Einzelelemente bestehen aus keilartigen Ringen, die versetzt aufeinandergesetzt werden.
Bild 4: Ringfeder Elemente, die gleichzeitig federn und dämpfen
Klotter,K. (1955):Schwingungen. In: Hütte, Des Ingenieurs Taschenbuch. Berlin: W. Ernst&Sohn.
Peil,U. (1993): Baudynamik. In: Stahhlbau Handbuch,Band I Teil A. Stahlbau-Verlagsgesellschaft mbH, Köln.
Petersen,C. (1996): Dynamik der Baukonstruktionen. Friedr. Vieweg&Sohn, Braun-schweig, Wiesbaden, 1996.
Petersen,C. (2001): Schwingungsdämpfer im Ingenieurbau. Herausgeber: Firma Mauer und Söhne, GmbH und Co KG, München.
Pritchard, B.P.: The use of shock transmission units in bridging. Proc,. Instn. Civ. Engrs. Structs&Bldgs, 1996,116, p.82-95.
Bei nicht zu großen notwendigen Dämpfungswerten werden heute gern sog. Flüssigkeitsdämpfer eingesetzt. Eine Flüssigkeitsmenge in einem rechteckigen oder runden Behälter wird mit einer (nicht gefrierenden !! ) Flüssigkeit so weit befüllt, bis die Schwappfrequenz gleich der Bauwerkseigenfrequenz ist. Diese hängt ab von der Beckenform und der Wassertiefe. Die beim Schwappen entstehende Anprallkraft wirkt in Gegenphase und deshalb wie eine Dämpfung. Der Verfasser hat vor Jahren den Einsatz solcher Dämpfer, die den Vorzug der Wartungsarmut haben, soweit numerisch aufbereitet, dass heute nur noch eine Excel-Tabelle aktiviert werden muss. Die Dämpfungswerte wurden dafür in Abhängigkeit der relevanten Parameter experimentell ermittelt und formelmäßig – d.h. in Abhängigkeit der maßgebenenden Parameter – in ein Excel-Arbeitsblatt formelmäßig bestimmt.
Die Frequenz einer in einem rechteckigen Behälter der Länge L_K mit einer Füllhöhe h_K (vgl. Bild 1)
Bild 1: Bezeichnungen Behälter und Schwingungsformen
schwappenden Flüssigkeit beträgt:
. …………………….. (1)
Eine Auswertung von Gleichung (1) für verschiedene Füllhöhen zwischen 200mm und 600mm variierende Beckenlängen ist in Bild 2 dargestellt.
Bild 2: Grundfrequenzen der schwappenden Flüssigkeit im rechteckigen Behälter
Scharparameter ist die Beckenlänge. g ist die Erdbechleunigung. Die Schwappfrequenz ist unabhängig von der Dichte der Flüssigkeit. Bei gleicher Füllhöhe sinkt die Schwappfrequenz mit zunehmender Beckenlänge.
Da das Verhalten der Flüssigkeit stark von den in Bild 1 dargestellten Eigenformen abweicht (es treten turbulente Zustände auf) soll das Verhalten mit Hilfe von Versuchen beschieben werden. Die in einem Behälter schwappende Flüssigkeit besitzt Eigenschaften, die denen eines Einmassenschwingers, wie er für das System eines Schwingungsdämpfers angenommen wird , ähnlich sind. So schwappt die Flüssigkeit nachdem das Becken angestoßen wurde, mit einer mehr oder weniger konstanten Frequenz hin und her. Die Amplituden der Wellenbewegung nehmen wegen der Eigendämpfung der Wellenbewegung mit der Zeit ab. Näherungsweise kann die Wasserbewegung deshalb mit einem System bestehend aus
beschrieben werden, vgl. Bild 3.
Bild 3: Mechanisches Modell für eine in einem Behälter schwappende Flüssigkeit
Eine solche Modellierung der Schwappbewegung wurde bereits 1957 von HOUSNER verwendet. Ziel der Versuche ist es, die vorstehenden Parameter mit Hilfe von in Schwingungsversuchen gewonnenen Messdaten zu identifizieren.
Die Versuche wurden im Institut für Stahlbau der Technischen Universität Braunschweig durchgeführt. Die Konzeption der Versuche basiert auf der Überlegung, das System Dämpfer vom Hauptsystem zu trennen und die Weggröße x(t) als Systemerregung vorzugeben. Die hierzu notwendige Erregerkraft F(t) ist die Summe aus Federkraft und Dämpferkraft sowie der Trägheitskraft der Totmasse. Werden der Systemeingang x(t) sowie der Systemausgang F(t) gemessen, können die freien Parameter des Dämpfersystems md, kd, dd so bestimmt werden, dass sich eine bestmögliche Übereinstimmung zwischen der gemessenen Erregerkraft und der auf Basis der identifizierten Parameter des Systems Dämpfer unter x(t) als Systemerregung berechneten Erregerkraft ergibt.
In Bild 3 ist die Prinzipskizze des Versuchsaufbaus dargestellt. Der Versuchsaufbau besteht aus folgenden Komponenten: a) Flüssigkeitsbehälter mit Wasserfüllung b) Linearlager aus Kugelgelenkbuchsenführungen c) Hydraulikzylinder d) Kraftmessdose e) Wegsensor f) Dehnungsmessstreifen
In Bild 4 ist der Aufbau bildhaft dargestellt:
Bild 4: Versuchsaufbau
Der Flüssigkeitsbehälter – mit konstanter Breite 300 mm – wird durch den Hydraulikzylinder auf einer quasi reibungsfreien Führung bewegt. Hierdurch ist es möglich, Frequenz und Amplitude der Bewegung zu steuern, um das Verhalten des Systems in verschiedenen Bewegungszuständen studieren zu können. Die Bewegung wird durch einen elektronischen Regelkreis als harmonische Bewegung mit konstanter Frequenz und Amplitude vorgegeben. Die eingestellte Amplitude wird nicht sofort, sondern linear zunehmend mit einer Geschwindigkeit von ca. 10 mm/s aufgebracht. Dir Regelung des Kraftzylinders wird so gesteuert, dass der Wasserbehälter eine sinusförmige Bewegung mit der Amplitude x-Dach und der Frequenz f machtvgl. Gl. (2)
. …………………… (2)
Die Kraftmessung wird mit einer Kraftmessdose der Fa. Hottinger durchgeführt. Diese ist in Reihe mit der Schubstange geschaltet. Auf deer Behälter-Rückwand wird ein Dehnungsmessstreigen geklebt, um die anschlagende Welle und deren Zeitpunkt messen zu können. Die Abtastung wurde mit einer Frequenz von 200 Hz durchgeführt.
Im folgenden Video ist ein Ausschnitt aus der Versuchsdurchführung zu sehen, Ein Wasserbehälter wird (nahezu reibungsfrei) von einer Schubstange geregelt bewegt. Die Bewegung wird von einem induktiven Weggeber gemessen. Der Weg wird sinusförmig vorgegeben, die dazu erforderlichen Kräfte werden über einen Kraftaufnehmer an der Schubstange gemessen.
Video 1: Versuch zur Ermittlung der Dämpfungswirkung bei einem Flüssigkeitsdämpfer
Zur Kalibrierung wurde ein Bezugsversuch ohne Wasserdurchgeführt. Die gemessene Kraft entspricxht im Wesentlichen den Trägheitskräften, die Reibkräfte bleiben vernachlässigbar klein. In Bild 5 sind zunächst die Rohmessdaten eines ausgewählten Versuchs graphisch dargestellt:
Bild 5: Rohmessdaten von Behälterweg x(t), Dehnung der Behälterwandung und Erregerkraft F(t)
Die Regelung über ein Servoventil erzeigt hochfrequente Kraftstöße. Diese sind im Kraftverlauf (unteres Teilbild von Bild 5 deutlich zu erkennen. Die Rohdaten wurden für die Weiterverarbeitung signaltechnsich aufbereitet, z.B. gefiltert (Bild 6) nd durch eine Fouriertransformation in der Frequenzbereich transformiert (Bild7).
Bild 6: Gefilterte Messdaten für Systemidentifikation
Es ist festzuhalten, dass sich die Kräfte aus dem schwappenden Wasser mit zunehmender Erregerfrequenz impulsartiger absetzen. Eine Fourier-Analyse der Erreger-kräfte ergibt deshalb, bei zunehmender Erregerfrequenz bezogen auf die theoretische HOUSSNER-Frequenz, auch ungerade ganzzahlige Vielfache der Eigenfrequenz.
 |
 |
| . | |
| Bild 6: Erregung unterhalb der HOUSNER-Frequenz… | Bild 7: Erregung oberhalb der HOUSNER-Frequenz. |
| . |
Offenbar wären also für hohe Erregerfrequenzen sowie große Wegamplituden weitere Freiheitsgrade für eine verbesserte Modellapproximation zu berücksichtigen. Darauf wurde hier allerdings verzichtet.
Im Rahmen dieser Untersuchungen soll jedoch lediglich das in Bild 3 dargestellte Einfreiheitsgradmodell identifiziert werden. Es wird deshalb eine weitere Tiefpassfilterung durchgeführt, deren Grenzfrequenz an die Grundfrequenz, bzw. an die Beckenlänge angepasst ist.
Es wurde ein großer Bereich der Parametern des Flüssigkeitsschwingungsdämpfers untersucht, um einen möglichst breiten Anwendungsbereich der Untersuchungsergebnisse sicherzustellen. Es wurden Beckenlängen zwischen L=200 mm und L=605 mm, Füllhöhen zwischen 100 mm und 250 mm, Schwingungsamplituden zwischen 5 mm und 80 mm, sowie relative Erregerfrequenzen zwischen 0,6 und 1,8 in den Versuchen eingestellt.
Zur mathematischen Beschreibung des Flüssigkeitsdämpfers wird von dem in Bild 8 dargestellten, linearen und stationären mechanischen Modell ausgegangen. Dieses Modell besitzt eine schwingfähige Masse und eine starre Masse, die sog. Totmasse. Beide Massen sind mit der Behälterwandung gekoppelt sind. Die Kopplung der schwingfähi-gen Masse erfolgt über ein lineares Feder- und ein viskoses Dämpferelement.
Bild 8: Modell des Flüssigkeitsdämpfers mit einem Bewegungsfreiheitsgrad
Das Modell besitzt vier Systemparameter (Ms, Mt, ks ,ds) und bei Vorgabe von x(t) einen Freiheitsgrad xs(t) und ist auch nach Untersuchungen von VERWIEBE bei kleinen Schwingungsamplituden im Allgemeinen ausreichend [Verwiebe1998]. Diese Aussage deckt sich auch mit den in Abbildung 2.6 dargestellten Ergebnissen.
Im Versuch werden die, für die vorgegebenen Weg-Amplituden x(t) notwendigen Erregerkräfte F(t) gemessen. Die Bewegung xs(t) der Schwappmasse Ms ist ebenso wie die Systemparameter unbekannt und kann nicht beobachtet werden. Die Bestimmung der unbekannten Systemparameter erfolgt durch iterative Anpassung und Vergleich der berechneten Erregerkraft mit der gemessenen Erregerkraft mittels des in Abbildung 3.1 dargestellten im Modells. 3.2.1 Randbedingungen Für die zu identifizierenden Parameter werden Grenzwerte festgelegt, innerhalb derer sich die identifizierten Parameter bewegen müssen. So wird verlangt, dass die Dämpfung ds und die Steifigkeit ks stets Werte größer Null annehmen müssen. Die Schwappmasse Ms wird als dynamisch äquivalente Masse nach HOUSNER vorgegeben:
. …………………. (3)
Eine Berücksichtigung der Schwappmasse als zusätzlicher Freiheitsgrad führte nicht zu einer verbesserten Modellbeschreibung.
In Abbildung 3.2 ist das Ergebnis der Systemidentifikation am Beispiel für einen Versuch und als Nachweis der Güte der Modellbildung dargestellt. Die identifizierten Parameter sind ebenfalls in der Abbildung 3.2 angegeben.
Bild 9: Vergleich der Messdaten und der Ergebnisse des identifizierten Versuchs
Einige Versuche mit L=605 mm und mit einer Beckenfüllung von 100mm, 120mm und 150 mm wurden zweimal wiederholt, um die Wiederholgenauigkeit sowohl der Versuchsdurchführung als auch der Systemidentifikation zu bewerten. Wie zu erwarten zeigten sich Streuungen der Ergebnisse, dies insbesondere im Bereich niedriger Erregerfrequenzen. Ohne hier weiter auf die Statistik der Versuchsergebnisse einzugehen soll noch ein Sicherbeiwert für die Dämpfungswerte bestimmt werden.
Die Festlegung eines Sicherheitsbeiwertes zur Berücksichtigung der Streuung für das Lehrsche Dämpfungsmaß kann deshalb gestaffelt erfolgen. Legt man den 5% Quantilwert (μ-1,65⋅σ) als Bemessungsniveau zugrunde ergibt sich bei einem Variationskoeffizienten von 20% – und Vorgabe eines Quantilwertes von 5% – ein Teilsicherheitsbeiwert von 
. ………………… (4)
Für die stärker streuenden Ergebnisse im Bereich geringer Frequenzen gilt dagegen:
. ………………….(5)
Es wird deshalb empfohlen die sich ergebenden Dämpfunsgmaße durch den Teilsicherheistbeiwert:
…………………..(6)
zu dividieren, um die versuchsbedingten Streuungen abzudecken.
Die Anhand der Systemidentifikation bestimmten Parameter des mechanischen Ersatz-modells sollen für die Entwicklung einer einfachen Bemessungshilfe durch eine algebrai-sche Lösung beschrieben werden. Wichtigster Parameter ist das Lehrsche Dämpfungsmaß. Beeinflussende Größen sind
. ……………… (7)
Bild 11: Excel-Arbeitsblatt zum einfachen Nachweis des gedämpften Schornsteins. Ein Ergebnis dieser Berechnung ist z.B. der in Bild 12 dargestellte Amplitudengang des gedämpften Hauptsystems (Schornstein).
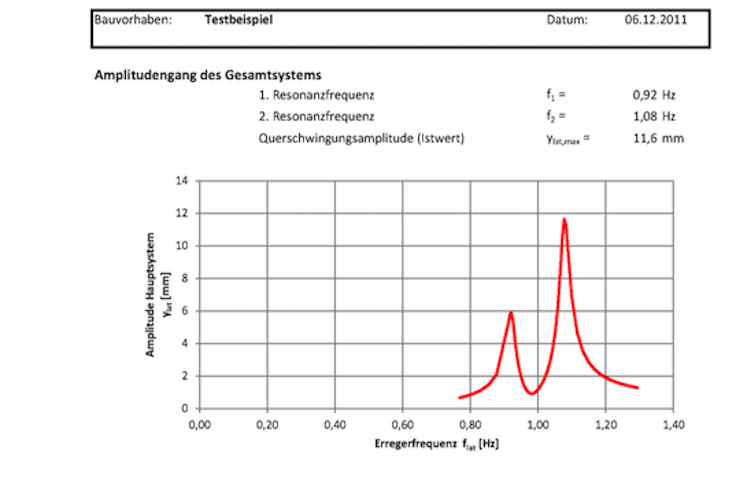
Bild 12: Amplitudengang des gedämpften Schornsteins
[Petersen1997] Petersen, C.: Stahlbau, Vieweg Verlag, 1997
[YU2010] Yu, J.-K.; Wakahara, T. & Reed, D. A.: A non-linear numerical model of the tuned liquid damper. Earthquake Engineering and structural Dynamics, 28, 671-686, 1999
[DINV4133] DIN V 4133: Freistehende Stahlschornsteine, Juli 2007
[DIN1055-4] DIN 1055-4: Einwirkungen auf Tragwerke – Teil4: Windlasten, März 2005
[Verwiebe1998] Verwiebe, C.: Grundlagen für den baupraktischen Einsatz von Schwingungsdämpfern auf Flüssigkeitsbasis. DIssertation RWTH Aachen, 1998
[Seber2003] Seber, G. A. F. & Wild, C. J.: Nonlinear Regression. Hoboken, NJ: Wiley-Interscience, 2003
[DuMouchel1989] DuMouchel, W. H. & O’Brien F. L.: Integrating a Robust Option into a Multiple Regression Computing Environment. Computer Science and Statistics: Proceedings of the 21st Sym-posium on the Interface. Alexandria, VA: American Statistical Association, 1989.
[Petersen2001] Petersen, C.: Dynamik der Baukonstruktionen, Vieweg Verlag, 2001
[Peil-1] Peil,U.: Baudynamik. In Stahlbau-Handbuch 1A, Stahlbauverlagsgesellschaft, Köln, 1993.
[Peil-2] Peil,U.: Baudynamik für die Praxis. In: Stahlbau-Kalender 2008, Hrgb. U. Kuhlmann, Ernst&Sohn, Berlin, 2008, p.390-476.
