Die richtige Abbildung eines realen Bauwerkes durch ein mechanisches Modell stellt in der Dynamik erheblich größere Anforderungen an den Ingenieur als im Bereich der Statik. Die Probleme ergeben sich z.B. daraus, dass bei der Modellbildung in der Dynamik i. Allg. keine Abschätzungen auf „sicherer Seite“ gibt, wie bei der Modellbildung in der Statik üblich, wo z.B. unklare Federbedingungen durch den Grenzfall „Gelenke“ ersetzt werden, um damit das System weicher als in Wirklichkeit zu machen.
Bei Einmassenschwingern wird man nur dann mit Grenzabschätzungen arbeiten können, wenn auf Grund der zu erwartenden Schwingungsphänomene klar ist, wie das Tragwerk reagiert. Bei komplexeren Mehrmassenschwingern ist die Abschätzung der Auswirkungen von Grenzannahmen für die höheren Eigenwerte i. Allg. nicht mehr möglich. Ziel einer genaueren dynamischen Modellierung muss deshalb sein, die Struktur so genau wie möglich durch ein Modell abzubilden. Zu steife Idealisierungen durch Ersetzen von elastischen durch starre Einspannungen oder zu grobe Elementierung durch Elemente mit vorgegebenem Verschiebungsansatz etc. führen zu größeren Fehlern und sind deshalb zu vermeiden. Die lokalen Beanspruchungsspitzen werden in der Regel durch höhere Eigenformen verursacht. Diese können sich aber nur dann annähernd wirklichkeitsgetreu einstellen, wenn das System im interessierenden Bereich genügend fein modelliert ist. Ziel einer genaueren dynamischen Modellierung muss deshalb sein, die Struktur so genau wie möglich durch ein Modell abzubilden.
Zu steife Idealisierungen durch Ersetzen von elastischen durch starre Einspannungen oder zu grobe Elementierung durch Elemente mit vorgegebenem Verschiebungsansatz etc. führen zu größeren Fehlern und sind deshalb zu vermeiden. Die Genauigkeit, mit der die Systemsteifigkeit modelliert wird, hängt darüber hinaus auch davon ab, wozu die späteren Ergebnisse der dynamischen Berechnung benötigt werden. Wenn lokale Schnittkraft- oder Spannungskonzentrationen bestimmt werden sollen, weil z.B. Ermüdungsuntersuchungen durchgeführt werden müssen, muss die Struktur mindes-tens genau so fein idealisiert werden, wie bei einer rein statischen Analyse. Die lokalen Beanspruchungsspitzen werden in der Regel durch höhere Eigenformen verursacht. Diese können sich aber nur dann annähernd wirklichkeitsgetreu einstellen, wenn das System im interessierenden Bereich genügend fein modelliert ist.
Ein wichtiger Punkt bei der Modellbildung des dynamischen Systems stellt die Modellierung der Anschlusspunkte im Stahlbau dar. Weiche Anschlüsse können das dynamische Verhalten erheblich verändern, die Eigenfrequenzen werden durch derartige Anschlüsse relativ stark beeinflusst. Wegen des relativ großen Einflusses auf den Gesamtenergiezustand findet man mit einer dynamischen Analyse (bei entsprechender Modellierung der Knotenpunkte, vgl. [21, 22, 23]) zwangsläufig alle Systeme mit weichen Anschlüssen, die oft Schwachpunkte der Konstruktion darstellen. Mit Hilfe einer begleitenden Bestimmung der Eigenfrequenzen kann deshalb auch eine rein statisch belastete Struktur konstruktiv oft verbessert werden.
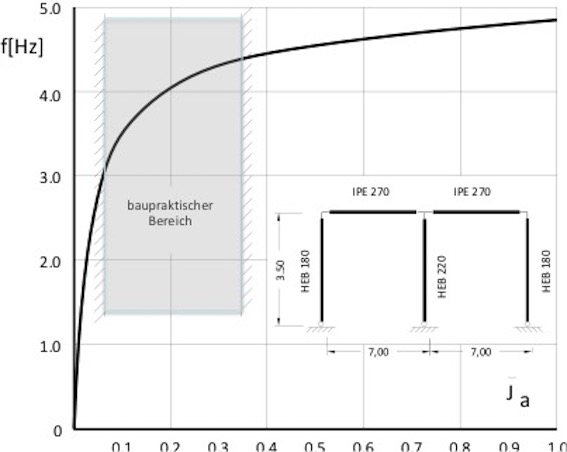
Im o.a. Bild ist das Verhalten für einen dreistieligen Rahmen dargestellt. Die Anschlussbereiche werden hierbei mit unterschiedlicher Steifigkeit modelliert. Die Erfassung der Anschlussweichheiten erfolgt nach [21]. Die Anschlussweichheiten werden durch kurze Stabelemente der Länge 0,1x L mit unterschiedlichen Steifigkeitswerten berücksichtigt. Über die genauere Behandlung der Anschlüsse von Rahmenecken, siehe [21,22,23]. Die Abszisse im Bild ist die Steifigkeit des Anschlussbereiches, bezogen auf den vollen Querschnitt des anzuschließenden Trägers. Man erkennt, dass die dargestellte 1. Eigenfrequenz des Rahmens mit sinkenden Anschlusssteifigkeiten stark abnimmt, vgl. dazu auch [22]. Die Eigenform ist hier nicht dargestellt, sie unterscheidet sich im baupraktisch üblichen Bereich praktisch kaum von der Eigenform des Rahmens mit starr verbundenen Stäben. Dies Ergebnis ist verallgemeinerbar: die Eigenformen verändern sich i. Allg. wesentlich schwächer als die entsprechenden Eigenfrequenzen.
Wenn bei Tragwerken höhere Eigenfrequenzen berücksichtigt werden müssen, weil z.B. die Erregerfrequenz hoch ist oder weil in der Erregerkraft-Zeitfunktion höhere Frequenzanteile enthalten sind, ist es unumgänglich, neben der Biegeweichheit auch die Schubweichheit zu berücksichtigen. Die höheren Eigenschwingformen sind durch eine Reihe von Nulldurchgängen gekennzeichnet, wodurch die fiktive Stützweite einer Halbwelle sehr kurz wird. Bei sehr kurzen, scheibenartigen Trägern ist der Einfluss der Schubweichheit bekanntlich sehr groß, so dass hierdurch die Eigenfrequenzen und -formen erheblich geändert werden können.
Man erkennt, dass die dargestellte 1. Eigenfrequenz des Rahmens mit sinkenden Anschlusssteifigkeiten stark abnimmt. Die Eigenform ist hier nicht dargestellt, sie unterscheidet sich im baupraktisch üblichen Bereich praktisch kaum von der Eigenform des Rahmens mit starr verbundenen Stäben. Dies Ergebnis ist verallgemeinerbar: die Eigenformen verändern sich i. Allg. wesentlich schwächer als die entsprechenden Eigenfrequenzen.
Zusätzlich erschwert wird die Modellierung der Systemsteifigkeiten dadurch, dass reale Anschlüsse oftmals keine lineare, sondern eine nichtlineare Federkennlinie besitzen, die Steifigkeit als von der Größe der Beanspruchung und der Beanspruchungsrichtung abhängt. Bei einer dynamischen Erregung werden verschiedene Niveaus der Beanspruchung durchlaufen, auch wechseln die Vorzeichen der Beanspruchung, so dass die Annahme einer konstanten Steifigkeit oftmals nur eine grobe Näherung sein kann.
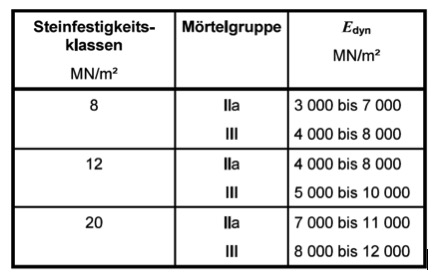
Der E-Modul von Stahl ist bei den im Bauwesen üblichen Schwingungen nicht von der Geschwindigkeit abhängig, so dass hier keine Unterscheidung zwischen statischer und dynamischer Beanspru-chung gemacht werden muss. Der E-Modul von Beton wächst bei dynamischer Beanspruchung. Näherungsweise kann mit einem um 10% vergrößerten, ideellen E-Modul gearbeitet werden. Die DIN 4178 „Glockentürme“ gestattet, wegen der vergleichsweise niedrigen Schwinggeschwindigkeiten, für Stahlbeton die statischen E-Moduln nach DIN 1045-1 in der Berechnung zu verwenden, gleiches gilt für Holz nach DIN 1052. Für Mauerwerk gibt die DIN 4178 dynamische E-Moduln an. Die oberen Grenzwerte sind 45% größer als nach DIN 1053. VGl. dazu das Folgebild:
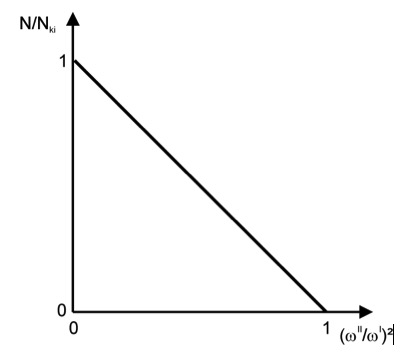
Bekanntermaßen besitzt eine Normalkraft Einfluss auf die Steifigkeit eines Tragwerkes. Eine Druckkraft verringert die Steifigkeit, eine Zugkraft vergrößert diese gegenüber dem Normalkraftfreien Zustand (vgl. Geigensaite). Ist die einwirkende Druckkraft so groß wie die ideale Knicklast, besitzt dass Tragwerk keinerlei Steifigkeit. Die Eigenfrequenz muss sich dann zu Null ergeben. Schätzt man den Einfluss diese Effektes mittels einer Dunkerlay-Gerade ab, siehe Folgebild folgt Gleichung: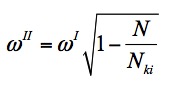 
.
Ein wichtiger Punkt bei der Modellbildung ist die Erfassung des Baugrundes. Wenn dieser nicht starr sondern elastisch ist, sinken die Eigenfrequenzen und die Dämpfung steigt.
Die Nachgiebigkeit der Gründung kann unter Umständen erheblichen Einfluss auf die Schwingfrequenz haben. Vor allem die Grundfrequenz von Türmen und Schornsteinen ist hiervon betroffen. Im Folgebild ist ein Beispiel von PETERSEN aus [2] dargestellt.
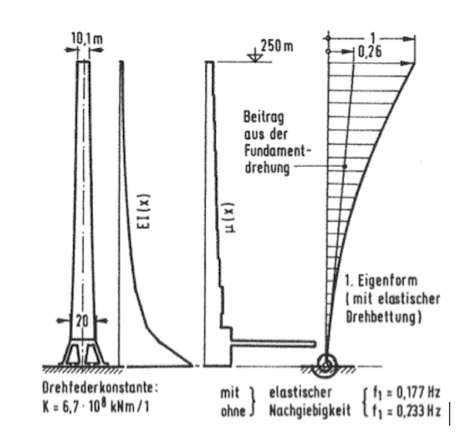
Die Frequenz der Grundschwingung reduziert sich durch die als elastische Drehfeder modellierte Fundamentsteifigkeit auf 75% des starr eingespannten Wertes. Dies kann dramatische Auswirkungen auf die Dynamik haben, z.B. bei Böenwindbelastung, bei der die Prozess-Energie bei niedrigen Frequenzen stark ansteigt.
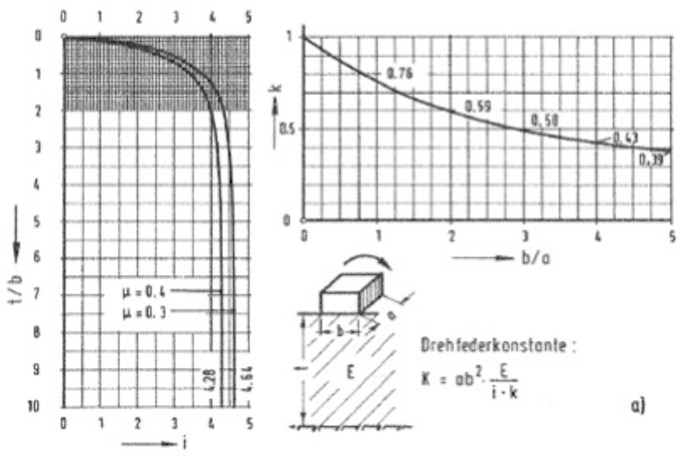
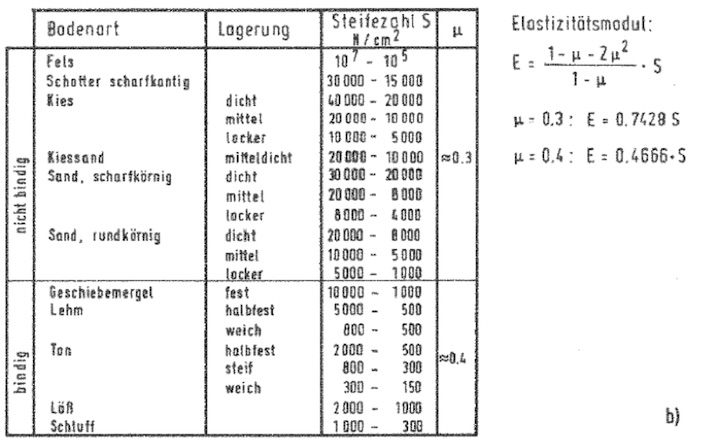
In [2] gibt PETERSEN Hilfsmittel an, mit denen die Drehfederkonstante abgeschätzt werden kann. Dem Folgebild kann für unterschiedliche Bodenarten und Fundamentgeometrien die Drehfedersteifigkeit entnommen werden.
 |
 |
Überall dort, wo größere Massen vorhanden sind, müssen bei einer genaueren Systemmodellierung z.B. mit Hilfe von Stabwerksprogrammen auch Knotenpunkte eingefügt werden. Die Masse ist ein im üblichen Bauwesen selten verwendete Einheit. In der Regel wird dort mit Gewichtskräften, dies sind gemäß Newtonschem AXiom die Massen mal der Erdbeschleunigung: F=a x M. Wenn im kN,m,s System gerevhnet wird (vergleiche dazu Dynamik/Grundlagen), was im Bauwesen üblich ist, ist die zugehörige Masseneinheit die Tonne, vgl. auch die Beziehung zwischen Kräften und Massen:
.
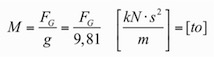Wenn z.B. Hochhäuser exzentrische Massen aufweisen, ist die Berücksichtigung der Exzentrizitäten sehr wichtig, da hiedurch ggf. Torsionsschwingungen ausgelöst werden können, mit Eigenfrequenzen im kritischen Belreich.
Eine Verteilung der großen Massen auf entfernte Knotenpunkte kann zu beträchtlichen Fehlern in der Berechnung führen. Im Regelfall ist die Struktur nicht nur mit ihrer eigenen, tragenden Strukturmasse behaftet, sondern sie trägt zusätzliche „tote“ Massen. Typisches Beispiel hierfür sind z.B. Turbinentische, auf deren Tisch“platte“ die Turbine und der Generator befestigt sind. Wenn diese Zusatzmassen größer sind als ca. 5% der Strukturmasse, sollte die Verteilung der Zusatzmasse auf das System genauer berücksichtigt werden. Hierfür müssen dann zusätzliche Knotenpunkte in die Struktur eingefügt und ggf. auch die Eigenbiegesteifigkeit der Zusatzstrukturen, wie z.B. der Turbinenwelle, berücksichtigt werden. Wenn Massen exzentrisch angreifen, kann die Exzentrizität durch steife Koppelelemente, wie z.B. biegesteife Stäbe simuliert werden, die von der Hauptstruktur bis in den Massenschwerpunkt der exzentrischen Masse reichen.
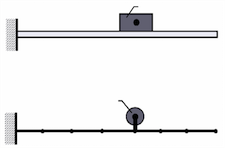
Mit einer Modellierung der Massenverteilung durch translatorische Einzelmassen (lumped masses) können nur die untersten Eigenwerte hinreichend genau bestimmt werden. Die hierbei erzielte Genauigkeit wird in vielen praktischen Fällen ausreichen. Wenn auch höhere Frequenzen interessieren, wird mit sog. konsistenten Massenmatrizen gearbeitet, mit deren Hilfe die Trägheitskräfte innerhalb des Elementes auf kinematisch äquivalente Knotenkräfte umgerechnet werden. Da hierbei Ansätze für den Verlauf der Beschleunigung über dem Element gemacht werden (bei den üblichen Stabelementen sind dies in der Regel Polynome 3.Ordnung), müssen die Stäbe feiner unterteilt werden, wenn höhere Eigenfrequenzen erfasst werden sollen.
Wenn Massen große Verdrehungen machen, kann auch die sog. Rotationsträgheit eine nicht unerhebliche Rolle spielen, vgl. das folgende Bild:
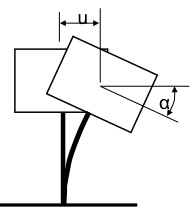
Die Rotation findest bei Biegung um den Massenschwerpunkt statt. Ersattzweise kann auch der elatische Schwerpunkt gewählt werden. Die Masse widersetzt sich dann nicht nur der seitlichen Verschiebung, sondern auch der Verdrehung. Für die Berechnung der Rotationsträgheit ist das sog. Rotations-Trägheitsmoment zu bestimmen. Es ist letztlich das Produkt der Masse mal dem senkrechten Abstand zur Drehachse zum Quadrat: . Allgemein gilt:
.
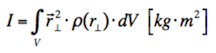Hierbei ist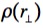 
die Masse am Ort 
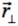. Dabei ist 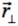der senkrechte Abstand von der Drehachse bis zum Masseteilchen, vgl. Bild;
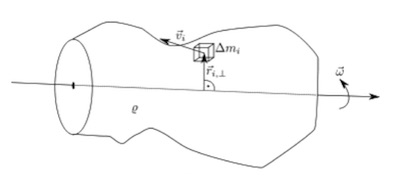
Bei Einzelmassen wird lediglich die Einzelmasse mit dem sekrechten Abstand zur Drehachse im Quadrat berechnet und alle Massenträgheiten werden aufaddiert. Die Berechnung erinnert an die Berechnung des Biegeträgheitsmomentes. Dort wird allerdings nicht die Masse zugrundgelegt, sondern ein Flächenelement. Die Rotationsmasse wirkt auf den Rotationsfreiheitsgraden.
Die dritte Struktureigenschaft, die passend beschrieben werden muss, ist die Dämpfung des Systems. Diese sorgt dafür, dass jede freie Schwingung nach einer gewissen Zeit zur Ruhe kommt. Verantwortlich für das Abklingen der Bewegung sind Einflüsse infolge von Gleitungen und Versetzungen in der Gitterstruktur des Werkstoffs (Werkstoffdämpfung), die zusammen mit der Dämpfung infolge von Reibungen an Verbindungsstellen (Systemdämpfung) etc. als sog. innere Dämpfung – d.h. als Dämpfung die das schwingende System selbst generiert – bezeichnet werden. Die innere Dämpfung wird in der Regel geschwindigkeitsproportional angesetzt.
Daneben tritt eine Kraftwirkung zwischen dem umgebenden Medium (Luft, Wasser) und dem schwingenden Tragwerk auf, die als äußere Dämpfung bezeichnet wird. Die Kraftwirkung entsteht durch den Formwiderstand c ·F der Einzelteile des sich im Medium bewegenden Tragwerks, sie ist der Bewegung stets entgegengesetzt und dämpft damit die Bewegung. Auch die äußere Dämpfung wird in der Regel geschwindigkeitsproportional angesetzt. Ein dritter Dämpfungsanteil ergibt sich aus der sog. Abstrahldämpfung. Dies ist die Energie, die in den Baugrund abstrahlt und damit für das System verloren geht.
Unter der inneren Dämpfung wird
verstanden.
Insbesondere die Baustoffdämpfung ist schwer zu beschreiben. Sie entsteht durch das nichtlineare Werkstoffverhalten, das seinerseits durch die erwähnten Gittergleichungen und Versetzungen (die eigentlichen Ursachen plastischer Verformung), sowie durch Schädigungen, wie z.B. Risse etc. hervorgerufen wird. Hierbei wird Energie vernichtet, so dass der Entlastungsweg nicht – wie bei elatischen Vorgängen – auf dem Belastungspfad liegt, vgl. Bild:
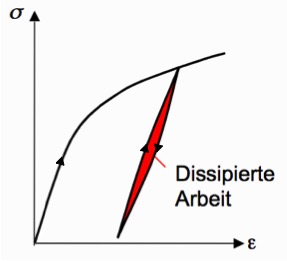
Bekanntlich ist die geleistete Arbeit bei einem Belastungs- oder die freigesetzte Arbeit bei einem Entlastungsprozess gleich der Fläche unter der Spannungs-Dehnungskurve. Dies verausgesetzt, sieht man, dass die Fläche unter der Belastungskurve größer ist, als die Fläche unter der Entlastungskurve. Es fehlt also Fläche, d.h. die bei der Belastung geleistete Arbeit wird nicht voll zurückgegeben. Es ist also Arbei verloren gegangen. Der Betrag an mechanischer Energie, der in jedem Zyklus durch die oben erwähnten Plastizierungen und Schädigungen etc. vernichtet wird, sie entspricht der rot gekennzeichneten Fläche der Hystereseschleife.
In dere folgenden Abbildung ist eine typische Spannungs-Dehnungskurve für einen Baustahl S235 unter höherer, zyklischer Beanspruchung mit den dabei typischen Hystereseschleifen dargestellt.
Aus den vorstehenden Erläuterungen wird klar, dass die innere Dämpfung mit steigender Beansprfuchung wächst. Wenn viele plastische Effekte oder innere Risse auftreten oder auch Reibungen an Schraubverbindungen initiiert werden, wird die Dissipation, d.h. Verschwinden von Arbeit deutlcih. Je größer die Dissipation, desto größer die Dämpfung.
Die Dämpfung kann näherungsweise aus den drei Anteilen Werkstoffdämpfung, Systemdämpfung und Abstrahldämpfung superponiert werden. Im Buch Baudynamik von Prof. Dr.Dr. Petersen sind entsprechende Werte angegeben. Ebenso sind im Programm StTools, das vom Institut für Stahlbau der TU Braunschweig vertrieben wird (httpss://www.stwind.stahlbau.tu-braunschweig.de) solche Werte angegeben und aufbereitet. Die Dämpfungswerte streuen in weiten Grenzen. Die Zahlenwerte, die in StTools angegeben sind (siehe folgendes Bild ), sind Mittelwerte nach [2]. In kritischen Bemessungssituationen sollte auch die Auswirkung von unteren und oberen Grenzwerten überprüft werden.
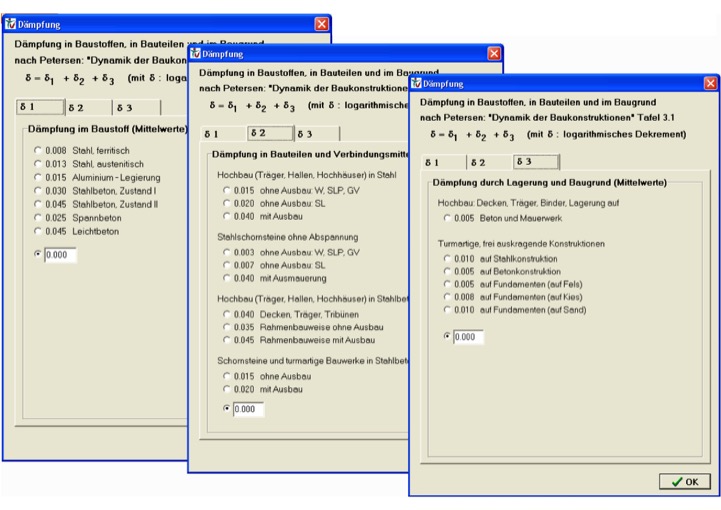
Wichtig: Wenn das nichtlineare Werkstoffverhalten bei der dynamischen Berechnung mit erfasst wird, wird die hieraus resultierende Dämpfung automatisch richtig modelliert. Man könnte auch Formulieren: Die Dämpfung ist ein (einfacher) Ersatz für die Berücksichtigung der ganzen System-Nichtlinearitäten.
Die Beschreibung eines derartigen Werkstoffverhaltens ist allerdings numerisch aufwendig. Der Aufwand resultiert vor allem aus der Notwendigkeit, bei der Ermittlung der Spannung stets die Beanspruchungsgeschichte mit auswerten zu müssen. Im Rahmen dieser Kurzdarstellung kann hierauf nicht weiter eingegangen werden.
Vielfach wird beim Entwurf vorgegeben, dass die Dämpfung nach Errichtung der Kontruktion zu ermitteln sei. Falls die bei der Berechnung angesetzetn Dämpfungswerte nicht erreicht werden, ist zusätzliche Dämpfung zu installieren (Siehe dazu Beherrschung). Die Dämpfung kann auf zwei Wergen bestimmt werden:
Es ist festzuhalten, dass eine direkte Messung des Dämpfungswertes in der Dimenion [kN/(m/s))=kN x s/m] nicht möglich ist, Dies kann man ggf. nur bei diskreten Dämpferelementen, wie z.B. Stoßdämpfern, durchführen. Alle Messungen an der Struktur schließen rückwärts aus dem Schwingungsverhalten auf die im Sy<stem wirkende Dämpfung. Es ist also immer eine indirekte Messung.
Ermittlung aus der Abklingkurve Zunächst muss das Tragwerk in Schwingungen versetzt werden: Z.B. durch Aufschaukeln in Resonanz oder durch Anzupfen mit einem dann zu kappenden Seil. Anschließend wird die Abklingkurve aufgezeichnet. Wenn diese nicht kontinuierlich als Funktion vorliegt, wie z.B. bei Videomessungen, reicht es aus, die maximalen Ausschwingweiten der Schwingungsgrenzlagen, die z.B. mit Hilfe einer Videokamera gemessen wurden, verwendet werden. Entscheidend sind die Amplituden der Schwingungsgrenzlagen, wie immer die gemessen wurden.
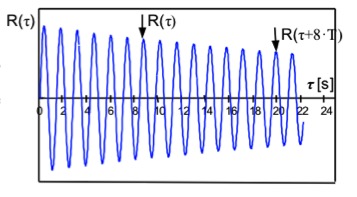
Nach Ermittlung der Ausschwingamplitude (kann i.d.R. aus ebenfalls im Video vermessenen, bekannten Systemabmessungen durch Dreisatz bestimmt werden) und ggf. Einzelbildfortschaltung, werden die Schwingungsgrenzlagen vermessen. Das logaritmische Dekrement der Dämpfung ergibt sich hieraus zu:
.
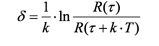Den „Trick“ nicht k=1 zu setzen und dann die aufeinander folgenden Schwingungsamplituden auszumessen, sondern k Schwingungen auszulassen, verwendet man gern, weil bei geringer Dämpfung die Unterschiede der Amplituden sehr gering sind (vgl. Bild), so dass der Fehler groß wird. Durch das Auslasse einiger Schwingungen (im Bild ist k=8), wird der Amplitudenunterschied größer, man muss dann natürlich das logarithmische Dekrement mit dem Faktor k korrigieren.
Ermittlung aus der Abklingkurve
Ein anderer Weg zu einer Messung der Dämpfung, besteht darin, die sog. Halbwertsbreite der Resonanzüberhöhungskurve auszumessen.
In der strukturdynamischen Berechnung schlanker Bauwerke oder Einzelbauteile ist eine möglichst genaue Kenntnis der zu erwartenden Systemdämpfung insbesondere gegen resonante Erregungsmechanismen unerlässlich. Aufgrund der vielfältigen und komplexen Mechanismen auf mikro- und makrostruktureller Ebene sind verlässliche Werte in der Ingenieurpraxis nur durch direkte Messungen oder aus direkt übertragbaren Erfahrungswerten zu erhalten.
Werte, für die in den Berechnungen anzusetzende Dämpfung, sind oftmals in den jeweiligen Normen angegeben, z.B. DIN 4178 „Glockentürme“, DIN 4133 „Stahlschornsteine“ etc..
Wird ein Tragwerk mit der Finite-Elemente-Methode diskretisiert, muss eine ausreichend große Anzahl an Elementen verwendet werden, um eine Lösung zu bekommen, die nahe an der exakten Lösung liegt. Ist es bei einer statischen Berechnung ausreichend das Konvergenzverhalten für bestimm-te Verformungswerte zu betrachten, sollte dies bei dynamischen Berechnungen für die Eigenwerte durchgeführt werden. Im fo9lgenden Bild ist das Ergebnis einer Untersuchung aus [31] dargestellt. Auf der Abszisse ist die Anzahl der verwendeten Elemente und auf der Ordinate die Abweichung von der exakten Eigenfrequenz dargestellt. Wie zu erkennen, steigt die Anzahl der für eine gute Approximation notwendigen Elemente mit steigender Eigenform an. Genügt bei der Berechnung der Grundschwingungsform noch eine Diskretisierung mit zwei Elementen, sind für die 4. Eigenform schon 16 Elemente notwendig.
Erfolgt die Lösung für beliebige Erregung mittels numerischer Integration der Bewegungsgleichung, sind auch hinsichtlich der Diskretisierung der Zeit gewisse Randbedingungen einzuhalten. So kann z.B. unterschieden werden zwischen impliziten und explitziten Integrationsverfahren. Die impliziten Verfahren nutzen für die Approximation der Zeitableitungen nicht nur die Zustandsgrößen der vorangegangenen Zeitpunkte, sondern auch den aktuellen Zeitpunkt i. Das Houboldt-Verfahren und das Newmark-Verfahren gehören zu den impliziten Integrationsmethoden, die zentrale Differenzenmethode hingegen ist ein explitzites Integrationsverfahren. Die impliziten Integrationsmethoden besitzen Vorteile hinsichtlich des numerischen Aufwandes bei nichtlinearen Berechnungen.
Eine weitere Unterscheidung kann man zwischen Einschrittverfahren und Mehrschrittverfahren treffen. Die Einschrittverfahren berechnen den Zustand des Tragwerks zum Zeitpunkt i+1 nur aus dem Zeitpunkt i, wohingegen die Mehrschrittverfahren mehrere weitere Zustände aus der Vergangenheit nutzen und so im Allgemeinen eine höhere Genauigkeit und Stabilität erreichen. Ein Integrationsverfahren ist stabil, wenn bei einem beliebigen Zeitschritt die Lösung nicht über alle Grenzen wächst. Viele kommerzielle Programme nutzen z.B. den Newmark-Algorithmus, der nur bei Wahl bestimmter Parameter und bei linearen Berechnungen ein stabiler Lösungsalgorithmus ist.
Durch die Wahl des Zeitschrittes wird darüber hinaus die Genauigkeit der Lösung beeinflusst. Hier ist allen Verfahren allgemein gleich, dass Sie sowohl die Antwortamplitude, als auch die Antwortfrequenz beeinflussen können. Die folgende Abbildung aus [32] zeigt für drei unterschiedliche Integrationsverfahren den Einfluss der Zeitschrittweite auf die Antwortperiode und die Antwortamplitude. Mit den drei Verfahren erreicht man eine hinreichend genaue Lösung, wenn die Zeitschrittweite 1% der Antwortperiode ist. Für baupraktische Untersuchungen ist es im Allgemeinen genau genug, als Zeitschrittweite delta_t = 1/20 der zur höchsten interessierenden Frequenz gehörenden Periode zu wählen.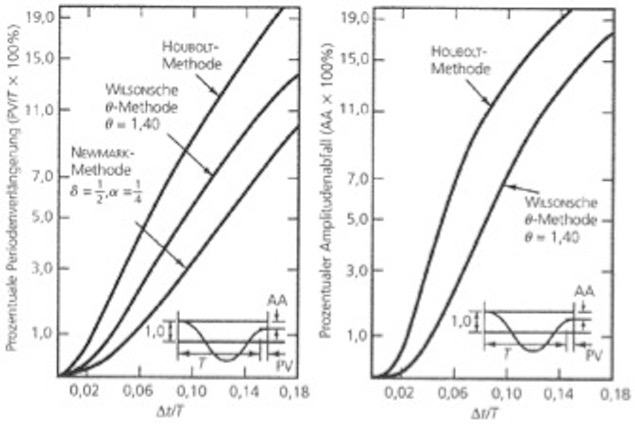 
Bei vielen Zeitschrittverfahren, so z.B. dem Newton.Verfahren tritt das delta_t auch auf der rechten Seite der Differentialgleichung, im Nenner des Massen- Lastgliedes sogar quadriert auf. Bei extrem kleinen Zeitschritten kann dies formal zu sehr großen dynamischen Lastanteilen führen, die die tatsächlichen äußeren Lastgrößen geradezu „zudecken“, d.h. die kleinen Größen der äußeren Belastung verschwinden im numerischen „Rauschen“ z.B. der sehr großen werdenden dynamischen Massen-Lastglieder.
[1] Den Hartog, J.P.: Mechanische Schwingungen. Berlin, Göttingen, Heidelberg: Springer 1952.
[2] Petersen, C.: Dynamik der Baukonstruktionen. Vieweg-Verlag, Braunschweig 1996.
[3] Peil,U.: Baudynamik. In. Stahlbauhandbuch 1, Teil A, Seite379-451. Stahlbau-Verlagsgesellschaft, Köln 1993.
[4] Hagedorn, P., S. Otterbein: Technische Schwingungslehre, Bd. 1 und 2. Berlin, Heidelberg, New York: Springer 1987.
[5] Klotter, K.: Technische Schwingungslehre I. (2. Auflage) Berlin, Göttingen, Heidelberg: Springer 1960.
[6] Klotter, K.: Schwingungen. In: Hütte, Des Ingenieurs Taschenbuch. Berlin: W. Ernst & Sohn 1955.
[7] Rausch, E.: Maschinenfundamente und andere dynamisch beanspruchte Konstruktionen. Düsseldorf: VDI-Verlag, 1959.
[8] Eibl, J., O. Henseleit, F.-H. Schlüter: Baudynamik. In: Betonkalender 1986.
[9] Müller, F.P.: Baudynamik. In: Betonkalender Teil 2, 1978.
[10] Waller, H., W. Krings: Matrizenmethoden in der Maschinen- und Bauwerksdynamik. Zürich: Bibliogaphisches Institut AG, 1975.
[11] Waller,H., R. Schmidt: Schwingungslehre für Ingenieure – Theorie, Simulation, Anwendung. Mannheim, Wien Zürich: BI-Wissenschaftverlag, 1989.
[12] Klingmüller,O., M. Lawo, G. Thierauf: Stabwerke, Matrizenmethoden der Statik und Dyna-mik, Teil 2: Dynamik. Braunschweig: Vieweg-Verlag 1983.
[13] Bachmann,H., W. Ammann: Schwingungsprobleme bei Bauwerken. Int. Vereinigung für Brücken und Hochbau (IVBH) ETH-Höngerberg, Zürich 1987.
[14] Petersen,C.: Schwingungsdämpfer im Ingenieurbau. Eigenverlag der Fa, Mauer & Söhne, München, 2000.
[15] Ruscheweyh,H.: Dynamische Windwirkung an Bauwerken. Band 1 und 2, Wiesbaden: Bau-verlag GmbH, 1982.
[16] Sockel,H.: Aerodynamik der Bauwerke. Braunschweig, Vieweg Verlag, 1984.
[17] Wahle,M.: Beitrag zur passiven Kontrolle schwach gedämpfter elastischer Strukturen mittels dynam. Schwingungsdämpfer. Diss. RWTH Aachen, 1984.
[18] Peil,U.: Bauen mit Seilen. In: Stahlbaukalender 2000. Ernst & Sohn, Berlin, 689-756.
[19] Peil, U.: Mast und Türme. In: Stahlbaukalender 2004. Ernst & Sohn, Berlin, 673-748.
[20] Tschemmernegg, F., F. Tauschnig: Zur Nachgiebigkeit von Rahmenknoten. Stahlbau 10 (1987),299-306 und 58 (1989),45-52.
[21] Sedlacek, G., M. S. Koo, G. Ballio: Behaviour of Steel Frames with Semi Rigid Joints under Seismic Induced Loads. In: Connections in Steel Structures,
Elsevier Applied Science Publishers LTD, 1988.
[22] Ermopulos, J., I. Vajas: Zum Nachweis von Rahmentragwerken mit verformbaren Knoten. Stahlbau 60 (1991),326-332.
[23] DIN 4131:1991-11: Antennentragwerke aus Stahl. Beuth Verlag GmbH, Berlin, 1991
[24] DIN 1055-4:2005-03: Einwirkungen auf Tragwerke – Teil 4: Windlasten. Beuth Verlag GmbH, Berlin, 2005
[25] DIN V 4131:2008-09: Antennentragwerke aus Stahl. Beuth Verlag GmbH, Berlin, 2008
[26] Peil, U. & Nölle, H.: Guyed Masts under Wind Load. Journal of Wind Engineering and Indus-trial Aerodynamics, S. 2129 – 2140, 1992
[27] Davenport, A. G.: The interaction of wind and structures. Engineering Meteorology, Hrsg. Plate, Erlsevier, 1982
[28] VDI 2038 Entwurf: Gebrauchstauglichkeit von Bauwerken bei dynamischen Einwirkungen, 2010
[29] Hamm, P.: Ein Beitrag zum Schwingungs- und Dämpfungsverhalten von Fußgängerbrücken aus Holz. Dissertation TU München, 2003
[30] Peil, U.: Dämpfung bei schlanken Zuglieder. Abschlussbericht zum DFG Forschungsvorha-ben PE 437/20-1
[31] Dinkler, D.: Baudynamik, TU Braunschweig, 1997
[32] Bathe, K. J.: Finite-Elemente-Methoden. Springer-Verlag, Berlin, Heidelberg, New York, To-kyo, 2002
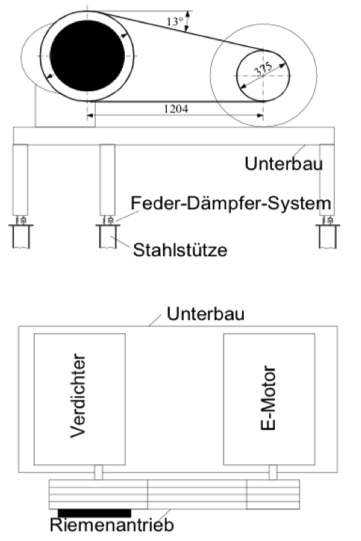
Zur Belüftung eines Bergstollens wird eine Zwangsbelüftung mit HIlfe eines Gebläses benötigt. Das Gebläse wird durch einben Elektromotor angetrieben. Motor und Gebläse sind auf einem Fundament angeordnet. Die Diffusorelemente sind statisch und dynamisch getrennt gelagert. Die Einwirkenden Kräfte sind zum einen die Eigengewichte der Elemente sowie die Erregerkräfte aus dem Motor plus Gebläse, d.h. Flügelrad. Die Kräfte ergeben sich aus einer plan- und unplanmäßigen Unwucht der rotierenden Teile. Die Werte für die Fliehkräfte des Betriebszustandes und des Zustandes Flügelrad mit einem gebrochenen Flügel (Störfall) sind vom Hersteller der Belüftung angegeben.
Das Bild zeigt das verwendete Fundament, der linke Klotz dient der Aufnahme der Difusorelemente, der Bock rechternhand sorgt für die Kraftübertragung der Maschinenkräfte in das Fundament. Die Dynamischen Erregerkräfte kreifen im Schnittpunkt der Stäbe an, dies ist die Drehachse des Motors.
Das Fundament wird auf einer 4cm Korkzwischenlage gelagert. Diese dient der Tiefabstimmung, vgl $$$$$$.
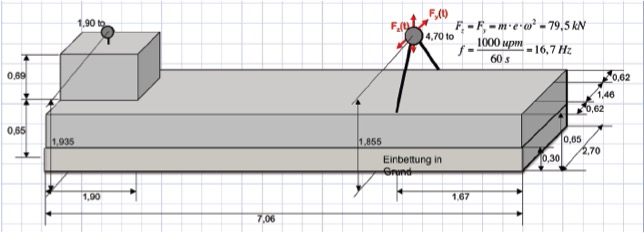
Der angesetzte E-Modul für die Bettung des Fundamentes setzt voraus, dass der Kork (Plattendicke 4cm), vor Einbau unter dem Fundament, mit etwa 25 kN/m^2 vorgewalkt wird. Hierbei werden harte Fasern zerstört und der Kork reagiert weniger steif. Bei Korkplattengrößen von 25x25cm entspricht dies z.B. einer Pressenkraft beim Vorwalken von 15kN. Die Korkplatten können in Stapeln vorgedrückt werden, vgl. dazu Rausch, S.70. Die Lagerungsdämpfung beträgt so: 
Das Dämpfungsmaß ist deutlich größer als 1, d.h. nennenswerte Schwingungen beim Durchfahren der Resonanzstelle sind nicht zu erwarten. Hinzu kommt noch die Dämpfung durch die Korkschicht, die immerhin auch im Bereich >15% log. Dekrement liegt (siehe Rausch, S. 70). ALlein diese hohe Dämpfung verhindert nennenswerte Resonanzampltuden im Störfall, d.h. beim Herunterfahren des Gebläses mit einem gebrochenen Flügelrad.
Die Eigenformen zeigen die Schwingunsganteile, in denen das Fundament sich bewegt. Man erkennt zwei typische Bereiche: +a. Eigenformen, (1-6) die durch diue weiche Korkfeder bestimmt sind, liegen unter 10Hz +b. Eigenformen, (>7) die zu einer Beanspruchung der Platte durch Biegung führen.
Diese liegen alle weit über 30 Hz.
Eigenformen in der Nähe der angreifenden Frequenz von 16,7 Hz treten nicht auf, so dass eine Resonanzanregung nicht auftritt. Außerdem würde das durch die große Dämpfung kein wesentliches Problem darstellen.
Der Umstand, dass die Erregerfrequenzen weit entfernt von den Resonanzfrequenzen liegen, ist der geschickten Abstimmung des Fubndamentes zu verdanken. Bedingt durch die große Masse und die weiche Korkfederung, ist das Systrem hier tiefabgestimmt, d.h. die anregenden Kräfte aus der Unwucht setzen sich im Wesentlichen mit der Massenträgheit ins Gleichgewicht und geben kaum Kräfte an den Boden ab.
Im Folgenden werden einige Eigenformen der verschiedenen Resonanzfrequenzen beispielhaft dargestellt,
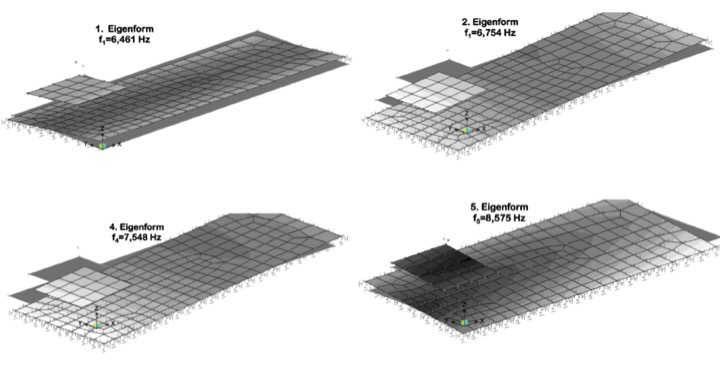
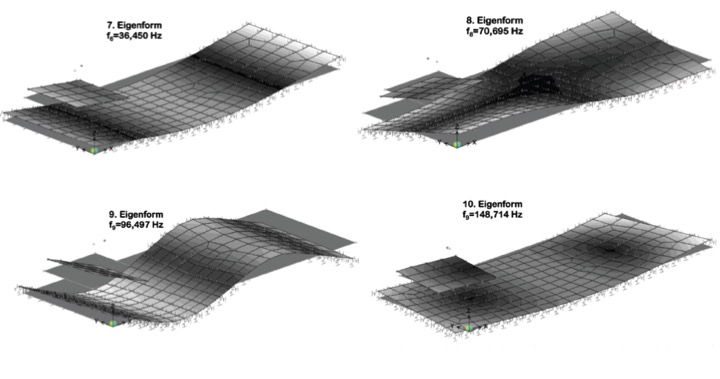
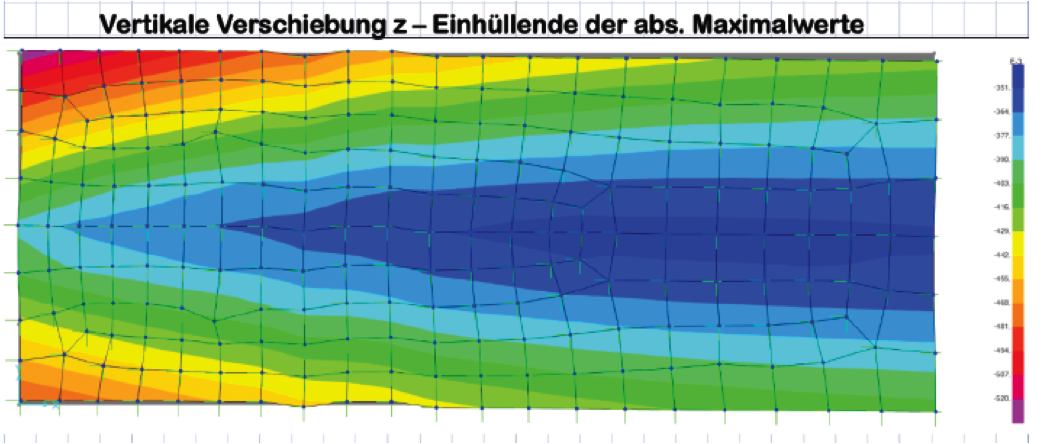
Im Folgenden werden die dynamischen Systemreaktionen unter der angreifenden Störfallbelastung F=79,5 kN ermittelt. Dabei wirken alle Eigenformen zusammen. Um die Ausgabe übersichtlich zu halten, werden die maximal Einhüllenden der absolut genommenen Vorzeichenbereiche dargestellt. Bei Momente können diese also in beiden Vektorrichtungen wirken, d.h. eine Bewehrung auf beiden betroffenen Seiten erfordern. Bei der Auswertung der Maimalwerte nach der Fehlfarbendarstellung am rechten Rand ist der Faktor zu beachten, der oben über der Farbleiste steht. Wenn alo z.B. die vertikale Verschiebung vz betrachtet wird, tritt am oberen linken Rand bei der lila Farbe der Wert 520 auf. Dimension ist bei Verschiebungen cm, bei Momenten kNcm. Es ergibt sich also im Störfall eine maximale vertikale Verschiebung von 520×10^-3=0,52cm=5,2mm. Das nächste Bild zeigt den Verschiebungs-Zeitverlauf im Störfall. Man erkennt die hohen Ausschläge nach Auftreten des Störfalls und das Einschwingen auf einen Schwingungsmodues mit zeitkonstanten Amplituden:
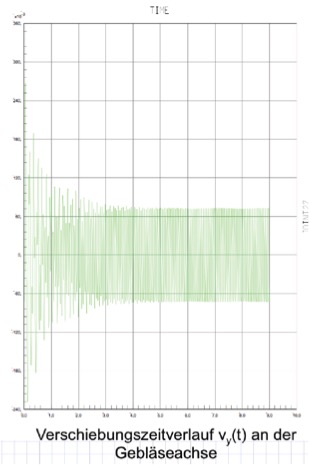
Das nächste Bild zeigt die Maximalwerte deer vertikalen Verschiebung in Falschfarbendarstellung:
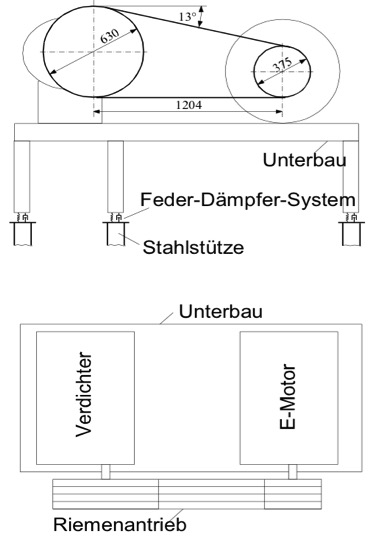
Die Welle eines sog. Brüdenverdichter einer Brauerei brach in fast regelmäßigen Abständen eines halben Jahres. Das folgende Bild zeigt den Aufbau:
Den Schliff der gebrochenen Welle zeigt das nächste Bild. Man erkennt deutlcih die sog. Rastlinien, die auf eine Ermüdunsgbelastung mit Pausen hinweisen, Man erkennt auch, wie die Rastalinien abstände nach rechts, also zur Gewaltbruchstelle hin immer größer werden. Der Bruchfortschritt geht also schneller vonstatten als zu Beginn. Dies leuchtet ein, da der tragender Querschnitt mit fortlaufendem Bruch immer kleiner wird und somit die bruchantreibenden Spannungen immer größer werden:
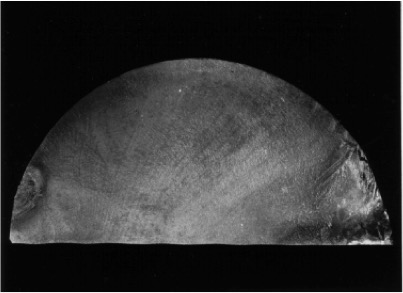
Da eine Demontage des laufenden Verdichters zum Zwecke der Installation von Messtechnik betrieblich nicht möglich war, wurde mit Hilfe eines Modells in den Verdichter „geschaut“. Das dabei verwendete einfache Modell ist im folgenden Bild dargestellt:
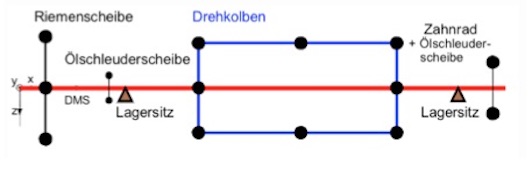
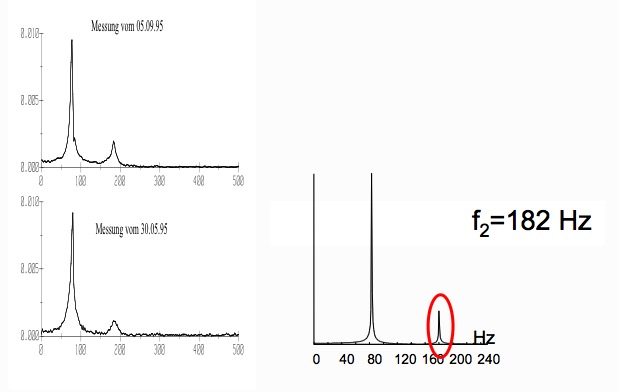
Mit Hilfe des Modells wurden die Maschineneigenfrequenzen ermittelt. Im folgenden Bild ist ein Vergleich der gemessenen und der gerechneten Frequenzspektren dargestellt. Man erkennt, dass das Modell das Verhalten ders Verdichters gut beschreibt, Die rot markierte Eigenfrequenz der maschine war kritisch, denn sie entsprech fast genau der sog. Zahneingriffsfrequenz von 182 Hz. Die Zahneingriffsfrequenz ist Anzahl der Zahneingriffe pro Sekunde. Sie ergibt sich einfach aus der Umdrehungsgeschwindigkeit des Verdichters und der Zahnanzahl. Bei jedem Zahneingriff wird also ein kleiner Stoß in Resonanz auf die Welle abgegeben, die dadurch zu Schwingungen erregt wurde und schließlich mit einem Ermüdungsbruch versagte.
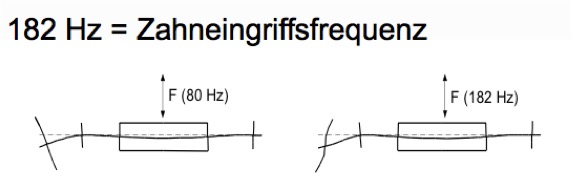
Das folgende Bild zeigt die Welleneigenformen bei den beiden Resonanzfrequenzen. Im Bereich der linken Lagerung ist die Krümmung besonders groß, hier treten also hohe Biegemoimente auf, die zu dem raschen Bruch der Welle führten:
Die Sanierung war nach Erkennen der Ursache relativ einfach. Der Verdichter musste verstimmt werden. Hierzu wurde außen auf der Riemenscheibe eien weitere dicke Platte montiert, die die Eigenfrequenzen ausreichend weit absenkte, so dass keine Resonanzgefahr mehr bestand. Das folgende Bild zeigt die Maßnahme schematisch:
