Am Abend des 21.07.1992 ereignete sich wÄhrend eines starken Gewitters ein Kettenschaden an der 380kV-Leitung Philippsburg-Pulverdingen in der NÄhe der Ortschaft Ubstadt / Bruchsal (Anlage 2). Durch den Bruch der Isolatoren fielen zwei der drei nördlichen 3-Phasen Leiter herunter und verfingen sich am Mastschaft bzw. an der Traverse. Hierdurch wurde ein Erdschluss ausgelöst. Da ein derartiger Schaden bisher als extrem unwahrscheinlich angesehen wurde, zudem der betreffende Tragmast zur Überquerung der Leiter über mehrere Bundesbahnstrecken sowie der Bundesstraße 3 dient, bat mich die Fa. ABB-Leitungsbau um eine gutachtliche Stellungnahme, in der die möglichen Ursachen des Schadens geklärt werden sollen.
Am 21.7.1992 gegen 20 Uhr wurde in der Schaltzentrale für die 380kV-Leitung Philippsburg-Pulverdingen ein Erdschluss registriert und die Leitung daraufhin automatisch vom Netz genommen. Die anschließende Besichtigung der Leitung zeigte einen Kettenschaden am Tragmast Nr. 46. Die die beiden nordöstlichen Leiterbündel tragenden Isolatorketten waren gebrochen. Die oberen Leiter hatten sich auf die untere Traverse gelegt, die unteren Leiter hatten sich im Mastschaft, etwa 10m unterhalb der 16m breiten unteren Traverse verfangen (Mastskizzen siehe Anlage 1).
Da der betreffende Tragmast in einem orographisch und topographisch komplexen Gelände steht, wurde eine Ortsbesichtigung vorgenommen. Der betreffende Tragmast steht unmittelbar am Rande des dort über etwa 40m teilweise steil ansteigenden Rande des Kraichgaus, Bild 1. Auf den Hang zu führt fast senkrecht die Neubaustrecke der DB von Mannheim nach Stuttgart, die im Hangbereich getunnelt ist. Die fast parallel zum Hang des Kraichgaus verlaufende DB-Strecke Bruchsal-Ubstadt verzweigt jeweils von Süden und von Norden ebenfalls in den Tunnel im Kraichgau-Hang. Der Bahndamm liegt im Bereich des Tragmastes ca. 14m über Grund. Der anschließende, hangseitige Mast ist ein Tragmast.
Bild 1: Topographische Übersicht
Am Nachmittag und Abend des 21.7.1992 ereigneten sich im Südwesten der Bundesrepublik schwere Gewitter mit starken Folgeschäden. In Anlage 6 bis 10 sind einige Zeitungsberichte Über das Ereignis beigefügt, welche die Schwere des Gewitters belegen.
Im folgenden wird zunächst die globale Wettersituation am 21.7.92 beschrieben, anschließend wird auf Messungen der Windsituation im Raume Bruchsal-Karlsruhe eingegangen. Da Gewitter örtlich eng begrenzt sind und Windmessungen im Bereich Ubstadt-Bruchsal nicht vorliegen, muss zur Abschätzung der wahrscheinlichen Windverhältnisse in Gewittern auf die Literatur zurückgegriffen werden.
Die im folgenden angegebene Analyse der synoptischen Bedingungen, der Windbeobachtungen und der Windverhältnisse in Gewittern wurde unter Mitwirkung des Diplom-Meteorologen S. Emeis, Hagenbach erstellt.
Grundlage der synoptischen Analyse sind die Berliner Wetterkarte, Amtsblatt des Instituts für Meteorologie der Freien Universität Berlin, Nr. 41-203 und der Europäische Wetterbericht, Amtsblatt des Deutschen Wetterdienstes, Jahrgang 17, Nr. 203.
Am Westrand eines Hochdruckgebietes Über Südosteuropa strömte sehr warme Luft von Süden nach Deutschland. Gleichzeitig hat sich am Morgen des 21.07.92 über der Bretagne aus einer Wellenstörung ein eigenständiges Tiefdruckgebiet gebildet, das nordostwärts zieht. Die Kaltfront dieses Tiefs liegt um 14.00 Uhr MESZ ungefähr 50 km westlich des Oberrheintales und erstreckt sich von Norden nach Süden. Der Tiefkern liegt bereits Über der Nordsee.
Östlich (vor) dieser Kaltfront liegen die Bodentemperaturen verbreitet über 30¯ C. In der Höhe (850 hPa-300 hPa) hat mit der Annäherung eines Höhentroges von Westen her am Mittag bereits Abkühlung eingesetzt. Diese Abkühlung in der Höhe führt zu einer fortschreitenden Labilisierung der Luftmassen über dem westlichen Deutschland. Um 14.00 Uhr MESZ melden Frankfurt und Gießen bereits Gewitter.
Die Bodenkaltfront und die Labilisierung kommen im Verlauf des Nachmittags ostwärts voran. Um 17.00 Uhr MESZ meldet auch Stuttgart ein erstes Gewitter und die Kaltfront Überquert den Rhein. Die Gewitter an dieser Kaltfront sind teilweise sehr heftig. Die Berliner Wetterkarte vermeldet aus Franken, Sachsen und Thüringen heftige Niederschläge und Sturmböen bis zu 28 m/s.
Die Stadt Karlsruhe bleibt von Gewittern weitestgehend verschont., so dass die Wettermeldungen von hier keine Besonderheiten enthalten (nur 3mm Niederschlag bis 20 Uhr MEZ) Nördlich und südlich der Stadt kommt es dagegen zu starken Gewittern (vrgl Anlagen 6 bis 10). Dies ist typisch für den eng begrenzten Bereich von Gewittern.
Die Windregistrierungen am 200m Mast des Kernforschungszentrums Karlsruhe GmbH, Institut für Meteorologie und Klimaforschung (ca. 10 km nördlich von Karlsruhe und 15 km südwestlich von Bruchsal gelegen) zeigen den Durchgang zweier mit Gewittern verbundener Böenlinien wenige Minuten vor 19 Uhr MESZ und wenige Minuten nach 20 Uhr MESZ (Tabelle 1, Anlage 12). Die über 10min gemittelte Windgeschwindigkeit in 40m Höhe Über Grund (das ist etwa 10-15m Über der Oberkante des Waldes, der das Kernforschungszentrum umgibt) beträgt bei der ersten Böenlinie 6,4 m/s, bei der zweiten 13 m/s. Die Windrichtungen sind beim ersten Durchgang 25¯ (Nordost) und beim zweiten Durchgang 224¯ (Südwest). Dies zeigt die stark variierende Windrichtung bei Gewittern.
Mit dieser Böenregistrierung ist der Durchgang zweier Gewitter nördlich von Karlsruhe belegt. Die Aufzeichnungen betreffen jedoch vermutlich nur die Randbereiche der Gewitter, deren Kerne weiter nördlich lagen.
Im folgenden sollen einige typische Winderscheinungen, die bei Gewittern auftreten, beschrieben werden. Da, wie bemerkt, keine direkten Messungen aus dem betreffenden Bereich vorliegen, muss hierzu auf die Literatur zurückgegriffen werden. Die hier vorgestellten Phänomene dürften so oder ähnlich auch bei dem schweren Gewitter im Bereich Ubstadt-Bruchsal aufgetreten sein. Bild 2 zeigt schematisch ein von links nach rechts ziehendes Gewitter. Rechts weht der Wind warme feuchte Luft auf das Gewitter zu. Links der Böenlinie stürzen beim voll entwickelten Gewitter mit dem fallenden Niederschlag (bei schweren Gewittern in der Regel mit Hagel) kalte, nahezu 100% wasserdampfgesättigte Luftmassen herab. Aus Kontinuitätsgründen muss sich diese Luft am Boden seitwärts ausbreiten. Die Vordergrenze dieser kalten Luft ist durch die eingezeichnete Kaltfront markiert und mit der Böenlinie identisch. In der herabstürzenden Luft und an der Böenlinie kommt es zu heftigen Turbulenzen.
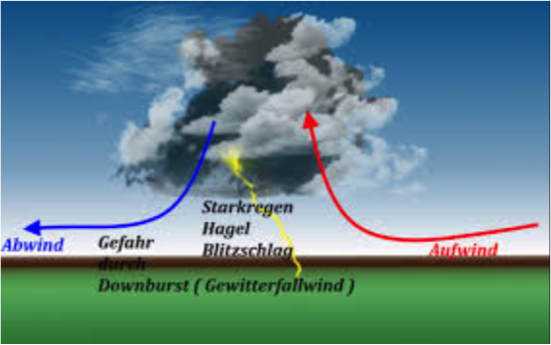
Bild 2: Typische Gewitterlage
Die Abwinde können in starken Gewittern eine vertikale Geschwindigkeit von 10m/s und mehr erreichen, sind aber örtlich eng begrenzt. In /2/ wird dargestellt, wie ein solcher Abwind in Bodennähe in eine horizontale Bewegung umgelenkt wird, wobei eine beträchtliche Vergrößerung der Geschwindigkeit stattfindet. Das Maximum liegt in dem gezeigten Beispiel in 50m Höhe über Grund bei 32 m/s. Die Böenlinie selbst schreitet mit etwa 14 m/s voran.
In /2/ wird auch eine schematische Darstellung der zu erwartenden maximalen horizontalen Windgeschwindigkeiten in Abhängigkeit von der horizontalen Ausdehnung der Gewitter gezeigt. Charakterisiert werden die Gewitter hierbei durch die Größe des mit ihnen verbundenen Hochdruckgebietes unter ihnen am Boden, welches mit der sich seitwärts ausbreitenden Kaltluftmasse , entstanden aus den kalten Abwinden, identisch ist. Für die typische Größe der hier in Frage kommenden Gewitter von ca. 10 km können demnach Spitzengeschwindigkeiten bis etwa 50 m/s erwartet werden.
Die synoptische Analyse hat gezeigt, dass am späten Nachmittag eine Kaltfront über Bruchsal hinweggezogen ist. Die Luftschichtung war labil und es kam zur Bildung heftiger Gewitter über Süd- und Mitteldeutschland. Windregistrierungen südwestlich von Bruchsal zeigen kurz vor 20 Uhr MESZ den Durchgang einer Böenlinie und damit ein Gewitter in direkter Nähe.
Auf Grund der geringen örtlichen Ausdehnung des Gewitters (von der Größenordnung 10 km) und des eigentlichen Abwindes (Größenordnung ca. 1 km), ist das über Bruchsal ziehende Gewitter von dem Messmast in Karlsruhe 15 km südwestlich nur am Rande erfasst worden. Spitzenböen von 30 m/s bis 50 m/s sind im Bereich derartiger Gewitter möglich. Das Windmaximum liegt ca. 50m über Grund, dies entspricht etwa der Höhe der betroffenen Leiter und Kettengehänge der betroffenen 380kV-Leitung. Die Windrichtung kann auf engstem Raum variieren.
Der bei Ubstadt verlaufende Abhang des Kraichgaus (Streichrichtung Nordnordost-Süd-Südwest) hat zusätzlich zu einer Kanalisierung der horizontal umgelängten Kaltluftmassen geführt. Da zum radialen Abströmen der horizontal umgelenkten Kaltluftmassen nur noch ein Kreissektor von ca. 180¯ zur Verfügung steht, steigen die Windgeschwindigkeiten weiter an. In grober Näherung (bei Anwendung des Satzes der Volumenkonstanz einer Strömung) etwa um den Faktor 2. Der „Abflussquerschnitt“ am Boden ist nur halb so groß, wie bei unbehinderter, allseitig radialer Abströmung in ein flaches Gelände, wie in /2/ vorausgesetzt.
Der im Bereich des Schadensortes senkrecht auf den Kraichgau-Hang zulaufende Bahndamm, auf dem u.a. die Neubaustrecke der DB von Mannheim nach Stuttgart in einen Tunnel geführt wird, hat im unmittelbaren Mastbereich vermutlich nicht wesentlich zur Steigerung der Windgeschwindigkeit beigetragen. Eine wesentliche Windverstärkung ist nur direkt über dem Bahndamm zu erwarten. Hieraus folgt jedoch, dass die anschließende Leitung zwischen dem Tragmast Nr. 45 und 46 im Bereich der Bahndammkreuzung erhebliche Zusatzbeanspruchungen erhalten hat, die auf die Beeinflussung durch den Bahndamm zurückgehen.
Im folgenden wird die Windverstärkung in Leitungshöhe über dem Damm grob abgeschätzt. In der Literatur (sowie in einem Vorschlag zur DIN 1055 Bl. 4 (Windlasten) sind Werte für Windgeschwindigkeitsverstärkungsfaktoren Über zweidimensionalen trapezförmigen Hügeln angegeben /15/. Die DIN-Werte liegen nach Messungen weit auf sicherer Seite, deshalb wird auf die Veröffentlichung /15/ zurückgegriffen.
Eingangswert für das Diagramm in Bild 3 ist die normierte Höhe über der Dammkrone. Diese ist abhängig von einem Längenparameter L, der gleich dem horizontalen Abstand von der Dammmitte bis zur Höhenkote mit halber Höhe ist. Der Wert L beträgt bei dem vorliegenden Damm ca. L=25 (in Windrichtung auf den Damm zu gemessen). Die Leitungen haben einen mittleren Höhenabstand über der Dammkrone von ca. 15m. Damit ergibt sich z/L=15/25=0,6. Aus Bild 1 folgt hieraus ein mittlerer Windgeschwindigkeitsverstärkungsfaktor von A=1,35. Ähnliche Verstärkungsfaktoren sind heute auch im Eurocode angegeben.
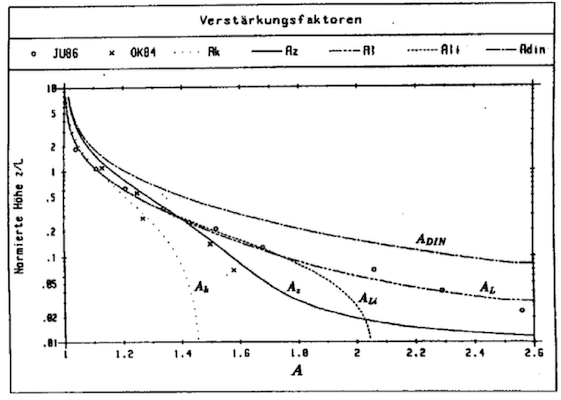
Bild 3: Windverstärkungsfaktoren über Hügeln
Da der Staudruck quadratisch mit der Windgeschwindigkeit wächst, wächst der Staudruck auch im Kreuzungsbereich Leitung-Dammkrone. Genauere quantitative Erkenntnisse können in Anbetracht der komplexen topographischen Situation jedoch nur Windkanalversuche erbringen.
Nach Wertung aller dargestellten Fakten erscheint eine von Nordnordost kommende Böe mit einer Windgeschwindigkeit von ca. 30 – 50 m/s an der Böenlinie des Gewitters über Bruchsal gegen 20 Uhr MESZ am 21.7.92 als realistisch. Bedingt durch die örtliche Topographie und die dadurch hervorgerufene Behinderung der Abströmung in Richtung Kraichgau, wird das im ungestörten Fall kreissymmetrische radiale Strömungsbild ovalisiert, mit einer Vergrößerung der Windgeschwindigkeit parallel zur Kante des Kraichgaus. Ein Böenspitzen-Windgeschwindigkeit entlang der Kraichgaukante im Bereich von 50 m/s erscheint hier realistisch. Im unmittelbaren Bereich der Kreuzung Bundesbahndamm-Leitung ist mit noch wesentlich vergrößerten Werten zu rechnen. In den folgenden Untersuchungen wird die lokale Vergrößerung über der Dammkrone vernachlässigt, es wird für genauere Berechnungen von einer Windgeschwindigkeit von 50m/s ausgegangen.
Die Abhängung der Leiter am Tragmast erfolgt über zwei parallele Stabisolatoren, die gelenkig an ein oberes Anschlussblech angeschlossen sind. Unten wird der LKeiter über ein Dreiecksblech, manchmal auch Herzblech genannt, angekoppelt. Bei der 380kV-Leitung sind die Kettenstäbe durch ein Zwischengelenk biegeentkoppelt. Dieses Zwischengelenk ist in Bild 4 nicht mit dargestellt. Bei seitlicher Windanblasung verschiebt sich das Isolatorgehänge parallelogrammartig (Bild 4). Bei einem kritischen Verformungswinkel α = 53 berühren sich die beiden Isolatoren. Das Gehänge blockiert und die zusätzlichen Windlasten werden über Biegung der Isolatorstäbe in die Traverse getragen. Biegebeanspruchung ist eine sehr kritische Art der Beanspruchung, Ketten sind in der Regel auf reine Normalkraftbeanspruchung ausgelegt. Der kritische Winkel beträgt nach Angabe von ABB bei der eingesetzten Kette α = 53°.
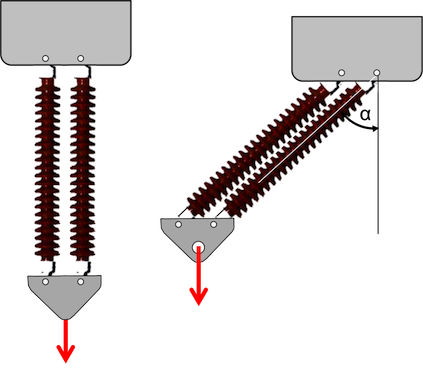
Bild 4: Kettenkinematik (unmaßstäblich)
Für die Berechnung der Kettenverformung wird u.a. der aerodynamische Kraftbeiwert der Leiterseile benötigt. Dieser wird nach nach den deutschen Normen DIN 4131 (Stählerne Antennentragwerke) und DIN 4133 (Stählerne Kamine) zu c=1,2 ) angesetzt. Dies ist jedoch ein oberer Grenzwert, der nur im unterkritischen Strömungszustand auftritt. Der Strömungszustand wird durch die sog. Reynolds-Zahl charakterisiert. Die Reynoldszahl ist bei kreisförmigen Querschnitten bekanntlich abhängig von
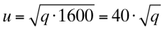mit dem Staudruck q in [kN/m^2]. Da der aerodynamische Kraftbeiwert bei größeren Reynolds-Zahlen absinkt, wird zur Abschätzung von der im Abs. 4.4 angegebenen maximalen Windgeschwindigkeit ausgegangen. Die sich ergebende Reynolds-Zahl deutet auf einen unterkritischen Strömungszustand hin. Die anzusetzenden aerodynamischen Kraftbeiwerte betragen hierfür (vgl. /7/ Bild 12.29) c=1,2..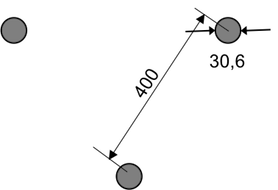
Bei derartig großen Abständen sind die aerodynamischen Beeinflussungen der Seile untereinander sehr gering, es wird näherungsweise von drei unabhängigen Seilen ausgegangen. Bei geringen Neigungen des Windvektors gegen die Horizontale, die praktisch immer gegeben sind, wird das hintere Seil vom Nachlauf des vorderen Seils beeinflusst, der Windwiderstand dieses Seiles erhöht sich leicht. Im folgenden wird deshalb davon ausgegangen, dass die beiden vorderen Seile unabhängig mit ihrem vollen Windwiderstand wirken, das hintere Seile hat einen um 10% größeren Windwiderstand.
Für die überschlägliche Berechnung der Kettenverschiebung werden die Abstände zu den Nachbarmasten benötigt. Diese werden aus dem Längenprofil und der topographischen Karte entnommen. Der Abstand zu Mast Nr. 45 beträgt ca. 413m, der Abstand zu dem bereits auf der Kraichgau-Kante stehenden Mast 47 beträgt ca. 350m.
Zunächst wird die Berechnung nach den Lastansätzen der DIN VDE 0210 durchgeführt, die auch dem Originalentwurf zugrundelag. Es wird zu Beginn die Kettenauslenkung unter dem Staudruckansatz nach DIN VDE 0210 bestimmt. Die Windlast auf die Kette des Mastes Nr. 46 beträgt: W=429,6 [kN ].
Das Eigengewicht, das durch die Kette Übertragen wird, beträgt: G== 421,3 [ kN].
Der sich einstellende Winkel an der Kette ergibt sich zu
α = arctan (29,6 / 21,3) ~ 54°.
Dies entspricht etwa dem kritischen Kettenwinkel. Da bei der Berechnung von einem voll korrelierten Windprozess ausgegangen wurde, liegt die Berechnung (für die vorausgesetzte Windgeschwindigkeit) auf sicherer Seite. Zur näherungsweisen Erfassung der Korrelation kann nach DIN 4131, Abschnitt A 1.6 bei Einzugslängen grösser als 100m, von 60% des maximalen Staudrucks ausgegangen werden. Hiermit ergibt sich der Kettenwinkel zu:
α = arctan (0,6 * 29,6 / 21,3) ~ 40°.
Hierbei ist zu beachten, dass durch den Kanalisierungseffekt der Kraichgau-Kante eine Gleichrichtung der turbulenten Strömung auftritt, wodurch die Turbulenz abnimmt, die Korrelationslänge nimmt deshalb zu.
Das Bild ändert sich, wenn die in Abs. 4.4 zusammengefasste Windsituation zugrunde gelegt wird. Der zu der Windgeschwindigkeit von 50m/s gehörende Staudruck beträgt:
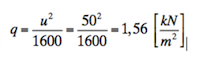
Der Kettenwinkel ergibt sich damit zu::
α = arctan (0,6 * 67,8 / 21,3) ~ 62°.
Dieser Wert ist deutlich grösser als der kritische Kettenwinkel. Bei der vereinfachten Berechnung wurde die mit wachsender Einflusslänge sinkende Korrelation näherungsweise gemäß DIN 4131 durch den Faktor 0,6 berücksichtigt.
Da zunächst vermutet wurde, dass das dynamische Verhalten des breitbandig angeregten Seiles zu laufenden Wellen, mit hoher örtlicher Beschleunigung am Verbindungspunkt Leiterseil – Isolator führt (Peitscheneffekt) und die hohen Beschleunigungen möglicherweise einen Biegebruch der Isolatoren verursachen können, wurde ein Leitungsausschnitt unter böiger Windeinwirkung nichtlinear dynamisch untersucht.
Darüber hinaus sollte hierdurch die Größe des Reduktionsfaktor 0,6 zur Erfassung der räumlichen Korrelation des Windes geprüft werden. Um über die tatsächlichen maximalen Auslenkungen unter turbulenter Windlast Aussagen zu erhalten, wurde eine nichtlineare dynamische Analyse zweier Felder durchgeführt. Durch die Randbedingungen der Unverschieblichkeit in Leitungsrichtung an beiden Enden wird ein Ausschnitt aus einer kontinuierlich abgehängten Leitung erfasst. Die Isolatorkette wird durch zwei in Reihe geschaltete Gelenkstäbe simuliert. Die parallelen Isolatoren wurden durch einen Stab ersetzt. Das System ist in Bild 6 dargestellt.
Bild 6: Untersuchtes Leiter- und Isolatorsystem
Die geometrischen Werte sowie der Durchhang wurden aus vorhandenen Zeichnungen entnommen. Abweichungen hiervon sind unkritisch in Bezug auf die Aussagekraft des Ergebnisses. Ebenso wie in den Überschlagsrechnungen wurde einer mittleren Feldlänge von 382 m ausgegangen.
Zur nichtlinearen dynamischen Berechnung müssen die Last-Zeit-Verläufe der Windkraft bekannt sein. Diese sind jedoch zufällig und deshalb nicht bekannt. Aus diesem Grunde wird ein Satz synthetischer Windgeschwindigkeitsverläufe generiert. Die Windgeschwindigkeitsverläufe haben die gleichen statistischen Eigenschaften wie der natürliche Wind. So entspricht z.B. die Varianz der einzelnen Windgeschwindigkeitsverläufe einer vorzugebenden Größe, die Korrela- tionsbeziehungen, beschrieben durch Auto- und Kreuzkorrelationen, entsprechen weitestgehend den beobachteten Korrelationen des natürlichen Windes /8,9,10,11,12/. Die Generierung wurde mit Hilfe eines autoregressiven Verfahrens vorgenommen, das jeweils Teile benachbarter Windschriebe gewichtet mit einbezieht und einen zusätzlichen Phasenshift unter der Annahme einer Gleichverteilung berücksichtigt /14/. Das zugrundgelegte Windleistungsspektrum ist ein modifiziertes Davenport-Spektrum, dass in vielen Messungen bestätigt wurde (Bild 7) /11/.
Bild 7: Vergleich verschiedener Spektren
Das Spektrum ist im Gegensatz zum original Davenport-Spektrum höhenabhängig. Da für die praktische Berechnung zwar Autospektren (z.B. gemäß o.a. Ansatz), aber nicht die Kreuzspektren direkt bekannt sind, kann die vertikale Kohärenz, einem Vorschlag von Davenport /6/ folgend, wie folgt bestimmt werden:
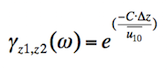
Darin ist:
Damit kann das Kreuzspektrum der Windgeschwindigkeiten bestimmt werden. Es ergibt sich:
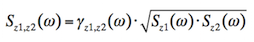
Da die Autoleistungsspektren unter der Wurzel reell sind, ist auch das sich ergebende Kreuzspektrum reell, die Fourier-Transformation in den Zeitbereich ergibt deshalb eine symmetrische Kreuzkorrelationsfunktion. In Bild 8 sind einige Kreuzkorrelationen dargestellt. Man erkennt, wie die Funktionen bei größerem vertikalen ABstand immer unsymmetrischer werden.
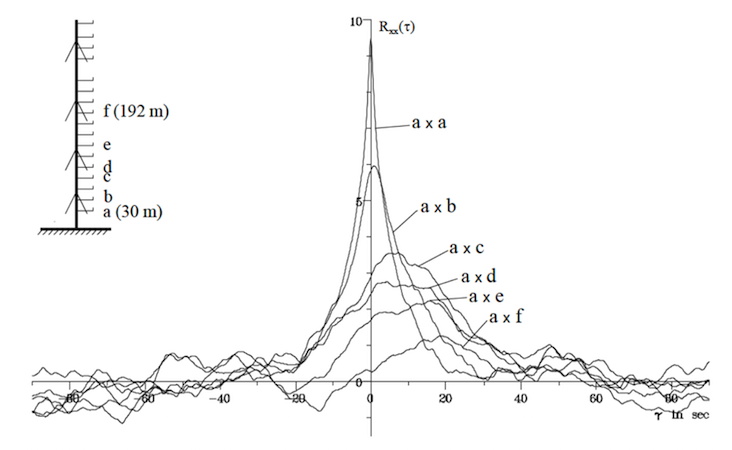
Bild 8: Autokorrelation- und Kreuzkorrelationsfunktionen
Für die Generierung wurde von folgenden Werten ausgegangen:
a) Mittlere Windgeschwindigkeit (Stundenmittel) in 10m Höhe: u_10 = 22 [m/s]
b) Exponent des Windgesetzes für die mittlere Windgeschwindigkeit: α = 0,28 , wegen der benachbarten Bebauung und der Dammsituation. Damit ergibt sich eine mittlere Windgeschwindigkeit in Höhe z=50m von v= 22 * (50/10) ^0,28 = 35 [ m/s] .
c) Standardabweichung des turbulenten Windanteils. Der rauhigkeits- und windgeschwindigkeitsabhängige Ansatz für die Standardabweichung des turbulenten Windanteils nach dem Ansatz von Davenport /6/ lautet:
.
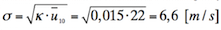Wegen des Gleichrichtereffektes in der kanalisierten Strömung wird die Standardabweichung des fluktuierenden Windanteils geringer. In den Berechnungen wird deshalb von einem reduzierten Wert von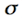 
= 5 m/s ausgegangen.
d) Abklingfaktor für die Kohärenzfunktion: C_y = 10,0 Wegen der zylinderartigen Böenform dürfte dieser Wert auf sicherer Seite liegen.
Die Windgeschwindigkeitsverläufe sind für einen Zeitraum von 2000 sec berechnet worden.
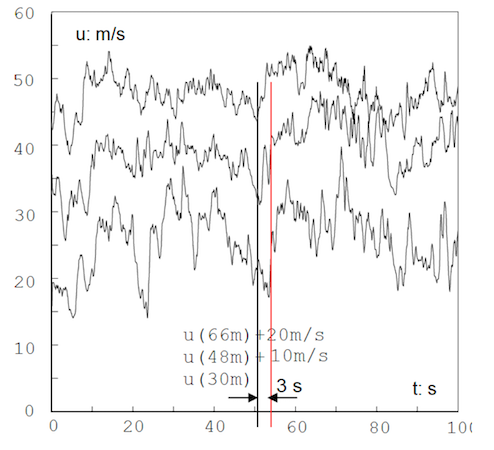
Die so gerechneten Windgeschwindigkeitsverläufe sind in Bild 9 dargestellt. Um ein ineinander zeichnen zu vermeiden, sind die Verläufe mit jeweils 20 m/s Abstand auf der Ordinate gespreizt dargestellt.
 |
 |
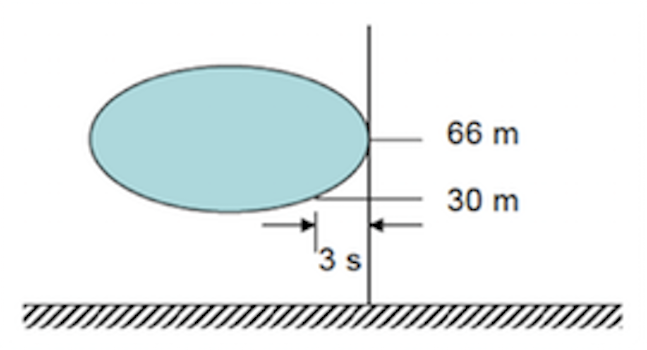| Bild 9: Generierte, korrelierte Windgeschwindigkeitsverläufe | Bild 10: Die Bezugslinie passierender Böenkörper |
Man erkennt deutlich die Korrelation in den Windschrieben, bei der am höchsten Punkt, hier 66m generierten Winggeschwindigkeit setzt gerade eine Böe ein, etwas später ist die Böe auch bei u=48m zu sehen und noch später bei u=30m. Der etwa kugelförmige Böenkörper schiebt sich langsam durch die betrachtete vertikale Messlinie, zuerst werden die oberen Punkte getroffen, wegen der Kugelform werden die unteren Punkte etwas später erreicht. Bild 10 macht dies deutlich:
Mit den so generierten Windgeschwindigkeitsverläufen wurde dann eine dynamische Berechnung durchgeführt. Die Materialdämpfung wurde hierbei mit dem Konzept der Rayleigh-Dämpfung erfasst, das berücksichtigte logarithmische Dämpfungsdekrement betrug im Mittel 0,01. Parallel wurde die aerodynamische Dämpfung berücksichtigt, indem stets die Differenzkomponente zwischen Windgeschwindigkeit und Eigengeschwindigkeit des Leiters als belastend angesetzt wurde. Das Stahl-Aluminium-Seil wurde durch ein Stahlseil modifizierter Fläche, aber gleicher Dehnsteifigkeit ersetzt.
Die Zeitschrittberechnung wird mit Hilfe des impliziten Newmark-Verfahrens durchgeführt. Wegen des nichtlinearen Verhaltens der Leiterseile muss in jedem Zeitschritt iteriert werden. Der Zeitschritt wurde zu 0,02 sec angesetzt um eine Beeinflussung durch höhere Eigenfrequenzen auszuschließen. Bei einer Zeitdauer von 2000 sec mussten also 100.000 Zeitschritte iterativ berechnet werden. Die Ergebnisse sind beispielhaft in den Bildern 11 bis 15 dargestellt.
Bild 7 zeigt für einen Ausschnitt den Querverschiebungsverlauf des unteren Isolatorpunktes. Man erkennt, dass die Ausschläge nach unten deutlich grösser sind als die Ausschläge nach oben. Dies ist durch die Nichtlinearität des Seilverhaltens bedingt.
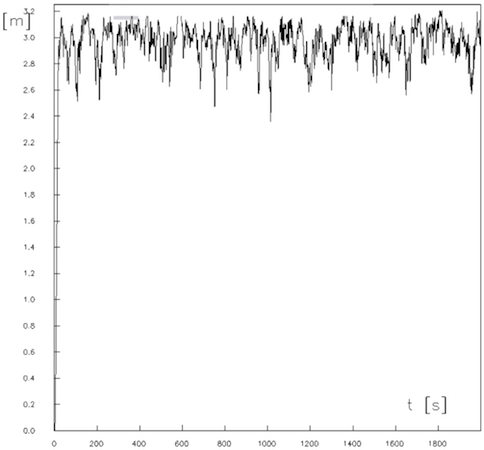
Bild 11: Querverschiebung des unteren Isolatorpunktes über der Zeit
Die maximale Querverschiebung beträgt ca. 3,27 m. Bei einer Isolatorlänge von 3,40 m beträgt der Ausschwingwinkel dabei α = arcsin (3,27 / 3,40) ~ 74°. Der Mittelwert der horizontalen Verschiebung beträgt ca. 2,95m. Hiermit ergibt sich ein mittlerer Ausschwingwinkel von
α = arcsin ( 2,95 / 3,40) = 60°.
Dies entspricht etwa den Ergebnissen der Näherungsberechnung mit dem Reduktionsfaktor 0,6 zur Erfassung der Korrelationen des Windprozesses (vgl. Abs. 2.2). Da der Windlastansatz nach Norm jedoch nicht vom (Stunden)-Mittelwert, sondern vom über 5 sec gemittelten Böenspitzenwert ausgeht, und dynamische Effekte nicht berücksichtigt werden, liegt der Normansatz offenbar auf unsicherer Seite.
Insgesamt bleibt festzustellen, dass bei genauerer Rechnung der Ausschwingwinkel grösser wird als bei den Näherungsberechnungen und Windlastansätzen nach Normen!
Bild 12 zeigt ebenfalls für einen Ausschnitt den Verlauf der Beschleunigung am unteren Isolatorpunkt. Man erkennt, dass die Beschleunigungen gering bleiben, maximaler Wert ist ca. 0,5 m/s 2 . Die Isolatorkette ist während der gesamten Zeit weitgehend gestreckt, Knicke treten nur begrenzt auf, wie auch Vergleiche mit dem Verschiebungsverlauf des Isolatorgelenkpunktes zeigen (Anlage 33). Ein Bruch durch hohe Beschleunigungsspitzen infolge von wellenartigen Schwingungserscheinungen (Peitscheneffekt) kann also ausgeschlossen werden.
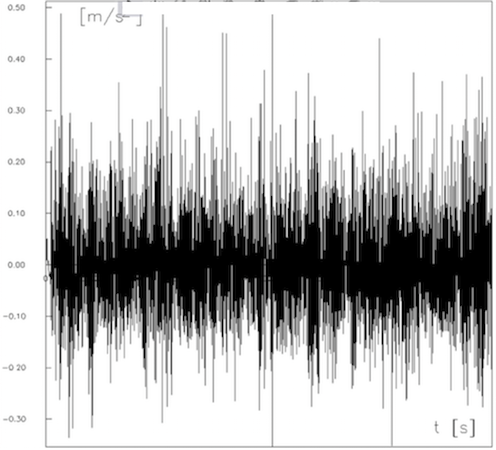
Bild 12: Beschleunigungsverlauf am unteren Isolatorende über der Zeit
In Bild 13 ist der Verlauf der Seilkraft des Elementes 7 am Isolatoranschluss dargestellt. Man erkennt, dass sich die Seilkraft beachtlich verändert, der Mittelwert liegt bei ca. 115 kN, der Extremwert erreicht ca. 170 kN.
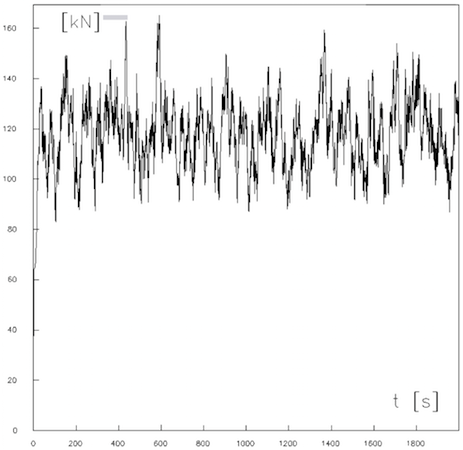
Bild 13: Seilkraftverlauf am Isolatoranschluss über der Zeit
Bild 14 zeigt die Längskraft in der Isolatorkette. Es ist zu beachten, dass wegen der Doppelisolatorausführung in Wirklichkeit jeder Isolator nur die Hälfte der Längskraft erhält. Die Isolatorkraft beträgt im Mittel ca. 44 kN, der Spitzenwert ist ca. 70 kN.
Zur Kontrolle wird die mittlere Isolatorlängskraft bestimmt. Die mittlere Windgeschwindigkeit beträgt ca. 35 m/s. Hiermit ergibt sich eine Windauflagerkraft am Isolator von W_A = 33,5 [kN].
Mit einer Eigengewichtauflagerkraft am Isolator von G_A =21,3 kN ergibt sich die mittlere Isolatorkraft durch geometrische Addition: N_Iso] = √ (33,5^2 + 21,3^2] ~40 [kN].
Das Ergebnis der dynamischen Berechnung entspricht in etwa der groben Abschätzung.
Durch die Bedingung, dass zu jedem Zeitpunkt die vertikale Komponente der Isolatorkraft gleich dem Ausgangseigengewicht sein muss, lässt sich die Rechnung einfach kontrollieren.
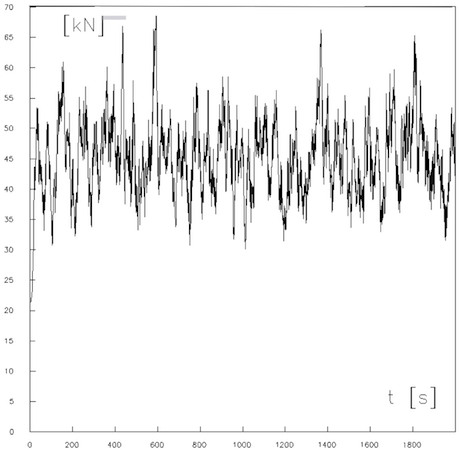
Bild 14: Isolatorlängskraftverlauf über der Zeit
Zur Identifizierung der beteiligten Frequenzen wurde der (vorab anti-aliasing gefilterte, um das anfangs von Null auf den Mittelwert anwachsenden Kurventeil (t=0 bis 20 sec) gekappte und mittelwertfrei gemachte) Zeitschrieb der horizontalen Verschiebungen des Knotens 7 mit Hilfe der Fast-Fourier-Transformation in den Frequenzbereich transformiert. Bild 15 zeigt das erhaltene Amplitudenspektrum. Man erkennt, dass sich der breitbandige Windanteil weitgehend durchsetzt. Neben einer starken Resonanzspitze bei f=0,18 Hz sind (wegen der Nichtlinearität) schwache Resonanzspitzen bei f=0,5 Hz zu erkennen. Die Resonanzspitze bei f=0,18 Hz entspricht der Pendelschwingung des Leiterseiles in Querrichtung. Die Pendelfrequenz eines durchhängenden Seiles ergibt sich bekanntlich zu:
f#4=#4 1 bruch [2#.l] #. wurzel [[S hoch [#2]] bruch m ]#4=#4 1 bruch [2#.382] #. wurzel [[115 hoch [#2]] bruch [0,00571]]#4=#4 0,185 Hz .
Wegen der in der Formel nicht berücksichtigten Isolatorabhängungen sinkt die tatsächliche Eigenfrequenz etwas ab.
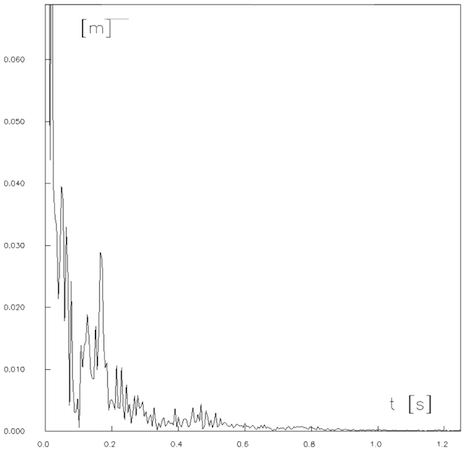
Bild 15: Amplitudenspektrum der horizontalen Verschiebung des unteren Isolatorpunktes
Beanspruchung des Isolators Der gebrochene Isolator stand für eine werkstoffkundliche Untersuchung nicht zur Verfügung, so dass über diesbezügliche Schadensursachen keine Aussage getroffen werden kann. Nach Angaben der Fa. ABB handelt es sich um einen Isolator mit 75mm Strunkdurchmesser. Die max. Längszugkraft im Isolator beträgt nach Bild 11 ca. 70 kN. Bei einer Querschnittsfläche des Isolators von A= pi#.7,5 hoch 2 / 4 = 44,1 cm^2 ergibt sich im Einzelisolator der Kette eine Längsspannung von
sigma tief = 1/2 * 70 / 44 ~ 0,8 kN/cm^2 = 8 N/mm^2 .
Die Starkstrom-Anlagen-Gesellschaft ermittelte in umfangreichen Prüfungen mit Langstabisolatoren eine Zug-Biege-Bruchdehnung von 1000 my m/m bei einer Versagenswahrscheinlichkeit von 50%. Für eine Versagenswahrscheinlichkeit von 1% beträgt die zulässige Dehnung 700 my m /m . Da die genannten Werte einer sekundären Veröffentlichung entnommen wurden, kann nicht gesagt werden, ob bei der zulässigen Dehnung von 700 my m /m ein Sicherheitsbeiwert berücksichtigt wurde. Hiermit ergibt sich laut /5/ eine zulässige Spannung von sigma = 35 N/m^2
Die vorhandene Spannung beträgt also etwa das 0,23-fache der zulässigen Spannung. Obwohl die zugrundeliegende Versagenswahrscheinlichkeit von 0,01 ein ungewöhnlich großer Wert ist (im Bauwesen wird mit Versagenswahrscheinlichkeiten von 0,0001 bis 0,00001 gerechnet), ist die Möglichkeit eines Isolatorbruches in Folge der ungewöhnlich hohen Windgeschwindigkeiten und zufällig sehr niedriger Beanspruchbarkeit des Isolators in Anbetracht des großen Abstandes zwischen Beanspruchbarkeit und Beanspruchung sehr unwahrscheinlich. Diese Aussage bezieht sich jedoch nur auf die üblichen Streuungen der Festigkeitswerte. Mögliche Fehlstellen oder vorhandene Beschädigungen des Isolators werden hierdurch nicht abgedeckt. Dies könnte durch eine Untersuchung des gebrochenen Isolators (sofern noch vorhanden) ggfls. überprüft werden.
Vergleich mit 110kV-Parallelleitung
Die unmittelbar benachbarte parallele 110kV-Leitung des Badenwerks und der Deutschen Bundesbahn ist nicht beschädigt worden. Im folgenden werden die Verhältnisse bei dieser Leitung abgeschätzt. Nach Angabe von ABB sind folgende Leiter eingebaut:
Die mittlere Einzugslänge beträgt ca.: l_m = (390+340)/2 = 365m.
Damit ergibt sich die Windkraft der Leitung der unteren Traverse bei einer vorausgesetzten Windgeschwindigkeit von 50m/s wie folgt:
W = 1,2 0,0224 365 1,56 0,6 = 9,18 [kN].
Die Eigengewichtslast beträgt: G = 0,00998 * 365 = 3,64 [kN ].
Damit wird der Kettenwinkel der unteren Leitung: α = arctan (9,18 / 3,64) ~ 69°.
Wegen des ungünstigeren Verhältnisses von Eigengewicht zu Windlast weht die untere Isolatorkette weiter aus als die der 380kV-Leitung mit 62¯. Allerdings sind hier die Hörner in Leitungsrichtung angebracht, so dass der kritische Ausschwingwinkel grösser wird.
Die Windkraft der Leitung der oberen Traverse ergibt sich zu:
W = 1,2 0,0245 365 1,56 0,6 = 10.04[kN].
Die Eigengewichtslast beträgt:
G = 0,01233 * 365 = 4,50 [kN].
Damit wird der Kettenwinkel der unteren Leitung:
α = arctan (10,04 / 4,50) ~ 65 grad.
Wegen des ungünstigeren Verhältnisses von Eigengewicht zu Windlast weht auch die obere Isolatorkette weiter aus als die untersuchte Leitung der 380kV-Leitung. Da hier die Hörner quer zur Leitungsrichtung angebracht, ergibt sich Angaben von ABB etwa der gleiche kritische Ausschwingwinkel.
Die Frage, warum nicht auch ein Kettenschaden bei der parallelen 110kV-Leitung aufgetreten ist, lässt sich auf Grund der ermittelbaren Tatsachen nicht direkt beantworten. Ein Grund wird in der Abschattungswirkung des 380kV-Leitungsmastes zu suchen sein, der im Abstand von 46m in Luv der 110kV-Leitung etwa parallel zur Kraichgau-Kante steht. Hierdurch ergibt sich (im Bereich der Tragmaste), bei einem geschätzen Völligkeitsbeiwert von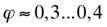 
eine Reduktion des mittleren Staudrucks auf ca. 80% bis 90% (vgl. Bild 13).
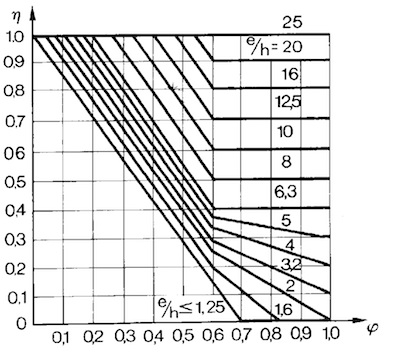Bild 13: Abschattung bei mehreren hintereinanderliegenden Tragwänden /7/
Daneben können auch die sehr starken vertikalen Richtungsänderungen der Gewitterwinde (siehe Abs. 4.4) eine Rolle gespielt haben, die zwar die 380kV-Leitung in voller Höhe getroffen haben, nicht aber vollständig auch die 110kV-Leitung.
Eine weitere Erklärung ergibt sich dann, wenn ggfls. weitere Untersuchungen des gebrochenen Isolators zeigen, dass der Schaden durch eine zufällig niedrige Festigkeit des Isolators der 380 kV-Leitung ausgelöst worden ist. Ein Isolator der 110 kV-Leitung mit mittlerer Festigkeit könnte dann ggfls. das Versagen verhindern. Ebenso könnte ein Isolator mit zufällig hoher Festigkeit an der 110kV-Leitung das extreme Windereignis Überstehen.
Bei der 380 kV-Leitung Philippsburg – Pulverdingen ist am 21.07.92, während eines starken Gewitters ein Kettenbruch aufgetreten. Die Auswertung der damaligen Windsituation ergab, dass sehr große Windgeschwindigkeiten aufgetreten sein müssen. Abschätzungen ergaben Windgeschwindigkeiten in ca. 50m Höhe von ca. 50 m/s. Bedingt durch die Kanalisierungswirkung der dort steil aufsteigenden Kante des Kraichgaus und die vorhandenen Dämme der Bundesbahn, sind noch höhere Windgeschwindigkeiten möglich. Dies gilt insbesondere für den Kreuzungsbereich der Leitung mit dem Bahndamm.
Vergleiche mit der Richtlinie DIN VDE 0210 zeigen, dass die dort verwendeten Staudruckansätze zu erheblich niedrigeren Windgeschwindigkeiten gehören. Der kritische Ausschwingwinkel des Doppelisolatorpaares wird bei Ausgang von den Staudrücken der DIN VDE 0210 eingehalten. Ein Vergleich mit den (vermuteten) tatsächlichen Windgeschwindigkeiten zeigt jedoch, dass hierbei der kritische Winkel deutlich überschritten wird.
Da zunächst vermutet wurde, dass das dynamische Verhalten des breitbandig angeregten Seiles zu laufenden Wellen, mit hoher örtlicher Beschleunigung am Verbindungspunkt Leiterseil – Isolator führt und diese einem Biegebruch der Isolatoren auslösen, wurde ein 2-feldriger Leitungsausschnitt unter böiger Windeinwirkung dynamisch untersucht. Es zeigt sich, dass die Beschleunigungen klein bleiben, so dass Schäden hieraus unwahrscheinlich sind.
Da der gebrochene Isolator für Untersuchungen nicht zur Verfügung stand, konnte zu Fragen der Mitverursachung des Schades durch Isolatoren mit zufälliger niedriger Festigkeit nichts ausgesagt werden.
Die unmittelbar benachbarte 110kV-Leitung ist auf Grund des Windwiderstand-Gewichtsverhältnisses geringfügig ungünstiger (in Bezug auf den maximalen Ausschwingwinkel) ausgebildet als die untersuchte 380 kV-Leitung. Da die Leitung nur 46m entfernt steht, hätte sich auch hier ein paralleler Schaden mit erheblicher Wahrscheinlichkeit zeigen müssen. Dies ist jedoch nicht der Fall. Erklärungen hierfür sind in der lokalen Windstruktur, insbesondere bei Gewittern, sowie in der Abschattungswirkung und den unbekannten Festigkeitswerten der Isolatoren zu suchen.
Zusammenfassend kann gesagt werden, dass der Schaden durch sehr hohe Windgeschwindigkeiten in einem starken Gewitter, in Verbindung mit der lokalen Topographie (Kraichgau-Kante, Bahndamm) den Schaden primär verursacht hat. Derartige Sommergewitter treten mit höherer Wahrscheinlichkeit auf, als der den Normen zugrunde gelegte 50-Jahreswind. Zwar ist die Wahrscheinlichkeit, dass ein bestimmter Ort von einem derartigen Ereignis wiederholt getroffen wird, wegen der geringen Ausdehnung eines Gewitters eher klein, irgend ein Mast der gesamten Leitung wird aber mit größerer Wahrscheinlichkeit getroffen, da die Leitung sich Über viele Kilometer erstreckt.
Wegen der speziell ungünstigen orographisch und topographischen Situation im Bereich des Schadensortes wird empfohlen, die Abhängung der Leitung am Mast Nr. 46, sowie an den beiden benachbarten Masten Nr. 45,47 so zu Ändern, dass auch größere Auswehungen zu keinem Schaden führen können. Diese Empfehlung bezieht sich auch auf die entsprechenden Maste der 110 kV-Leitung. 23( )
1 Browning et.al., 1976, Mon. Weath. Rev. 104, 603-610
2 Fujita,T.T., 1981, Journ. Atmos. Science, 38, 1511-1534
3 Simiu,E., R.H.Scanlan: Wind Effects on Structures. New York, J.Wiley & Sons, 1986.
4 Sockel,H.: Aerodynamik der Bauwerke. Baunschweig,Wiesbaden, Vieweg 1984.
5 Berechnung einer Teilkette bei Doppelisolatorketten. Dynamische Untersuchung Fa. Elektrowatt, Zürich, 1982.
6 Davenport, A.G.: The application of statistical concept to the wind loading of structures. Proc. Inst. civil Eng. Vol. 19., 1961
7 Sockel,H.: Aerodynamik der Bauwerke. Braunschweig, Vieweg Verlag, 1984.
8 Maier-Erbacher,J., E.J. Plate: Aerodynamische Belastung zylindrischer Bauwerke. SFB 210/ET/48, Universität Karlsruhe 1988.
9 Peil,U., H.Nölle: Windbelastung und dynamisches Verhalten abgespannter Maste. Vortrag auf den CEEC (Civil Engineering European Courses). Aachen, Lehrstuhl für Baustatik 1990.
10 Peil,U., H.Nölle: Measurement of Wind Load and Response of a Guyed Mast. Proc. Of the Eurodyn ’90 conf. Bochum 1990.
11 Peil,U., H.Nölle: Guyed masts under wind load. Journ. Wind Eng. and Industr. Aerodyn., 41-44 (1992) 2129-2140
12 Peil,U.: Baudynamik. In: Stahlbau-Handbuch Band I, 1993.
13 Peil,U., H.Nölle, ZH.Wang: Dynamisches Verhalten abgespannter Maste. VDI-Berichte 1992.
14 Peil,U., ZH.Wang: Generierung spektrumskompatibler und korrelierter Windgeschwindigkeitsverläufe. Erscheint demnächst.
15 Heldt,K.: Ermittlung von Windverstärkungsfaktoren für annähernd zweidimensionale Hügel. Berichtsheft des Sonderforschungsbereichs 210 zum Kolloqium am 7.10.1988, Karlsruhe 1989.
