Wenn in der Praxis störende Schwingungserscheinungen an Bauteilen oder Bauwerken auftreten, ist es zunächst wichtig, sich möglichst genaue Informationen über die Schwingungserscheinungen zu beschaffen, um Hinweise auf die möglichen Ursachen und damit auch für evtl. Sanierungsmaßnahmen zu erhalten. Im Vordergrund steht hierbei in der Regel, das Bestimmen der Eigenfrequenzen und ggf. der vorhandenen Systemdämpfung. Dies ist am einfachsten, wenn die Schwingungen gemessen werden können. Eine rein theoretische Behandlung ist im Regelfall nicht zu empfehlen, da hierbei durch die Wahl des Rechenverfahrens und der Systemmodellierung Vorgaben gemacht werden, die am Bauwerk häufig so nicht vorliegen und die deshalb zu falschen Schlüssen in Bezug auf die wahre Schwingungsursache führen können. Wenn dagegen Naturmessungen durchgeführt werden, kann mit den Ergebnissen ein theoretisches Modell identifiziert werden, so dass für weitere Berechnungen von gesicherten Voraussetzungen ausgegangen werden kann. Stets gilt die Regel, dass die direkte Messung einer Größe einer indirekten Messung vorzuziehen ist, da hierbei die größtmögliche Transparenz herrscht. Also: Verschiebungen messen, nicht aus Beschleunigungen integrieren. Fehlerquellen, z.B. durch numerische Fehler beim Umrechnen, entfallen. Weiterhin sollte man möglichst immer dort messen, wo große Messsignale auftreten, also z.B. besser in Feldmitte an den Schwingungsbäuchen als in Auflagernähe, wenn Wege, Geschwindigkeiten oder Beschleunigungen gemessen werden. Da bei jeder Messung auch zufällige Stör- oder Rauschsignale mit gemessen werden, wird hierbei das Verhältnis von Nutzsignal zu Rauschsignal groß. Jede durchgeführte Messung stellt einen Kompromiss zwischen Messkosten und er- wartetem Ergebnis dar. Wenn z.B. zur Beurteilung einer Schwingung lediglich die Resonanzfrequenz interessiert, reicht häufig ein Auszählen der Schwingung mit Hilfe einer Stoppuhr aus, wenn dagegen z.B. Zahlenwerte der Beschleunigungen oder der Beanspruchungen benötigt werden, wird man nicht umhin können, Messanlagen zu installieren. Im Folgenden sollen kurz die Vor- und Nachteile unterschiedlicher Messeinrichtungen dargestellt werden.
Bei der Auswahl der Messgeräte sollte man zunächst prüfen, ob eine direkte Mes-sung der Messgrößen gegen einen Festpunkt möglich ist oder nicht. Messungen gegen einen Festpunkt sind oft mit einfachen Mitteln, ohne Einsatz von Messelektronik, durchführbar. Messungen gegen einen Festpunkt sind auch berührungslos durchzuführen, indem z.B. Theodolithe, Nivelliergeräte oder moderne auf Laserbasis arbeitende Geräte eingesetzt werden, die am Gerätestandpunkt einen Festpunkt bilden.
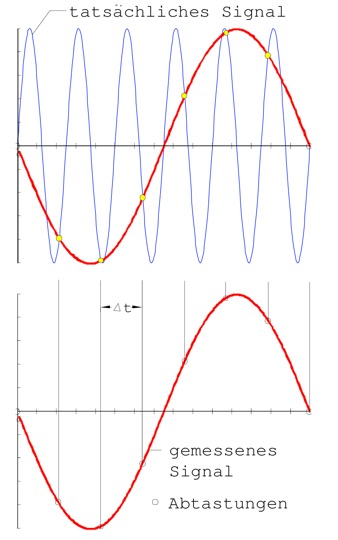
Wichtig bei Messungen ist eine hinreichend genaue zeitliche Abtastung des zu messenden Signals! Jede Schwingung muss mindestens zweimal pro Periode der höchsten zu bestimmenden Frequenz abgetastet werden, wenn kein wesentlicher Informationsverlust eintreten soll (Abtasttheorem von Shannon). Es gilt: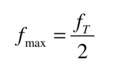 
Sind höhere Frequenzen als f_max im Zeitsignal vorhanden (die dann weniger als zweimal pro Periode abgetastet werden), so werden diese mit in das aktuelle Amplitudenspektrum hineingespiegelt und verfälschen es, man spricht von aliasing (lat. alias=fremd). Bekanntes Beispiel einer Unterabtastung ist das dückwärtslaufende Speichenrad einer Kutsche im Film: Wenn die Speichenwechselfrequenz größer ist als die Filmbildwechselfrequenz. Bei gleicher Frequenz des Speichenwechels und der Bildaufnahme scheint das Rad still zu stehen, da das Auge den Wechsel der Speiche nicht wahrnimmt. Man sollte die Grenze 1/2 f_T nie genau ausnutzen, sondern immer etwas Sicherheitsabstand hinzugeben, da die Regel 1/2 eine scharfe Rechteckfilterung voraussetzt. Diese ist in Realität aber nicht gegeben. Bei Verwendung von Videokameras muss man sich über die Bildwechselfrequenz informieren. Dies liegt in der Regel im Bereich von ca. 30 Hz, d.h. 30 frames pro Sekunde. Das bedeutet, dass man Frequenzen bis 15Hz besser ca. 10Hz noch einigermaßen gesichert aufnehmen kann. Im folgenden Bild ist die Problematik dargestellt. Das hochfrequente Zeitsignal wird zu grob, d.h. in größeren Abständen als es die FRequenz 172 f_T erfordert. DIe Abtastpunkte fassen irgendwo ins Signal hinein und produzieren so einen falschen Zeitverlauf (rot dargestellt):
Bei Messungen gegen einen Festpunkt werden bei Bauwerken i. Allg. die Schwing- wege bestimmt. Die Messungen können mit einfachsten Mitteln durchgeführt werden. Mit Hilfe einer Stoppuhr kann die Schwingungsfrequenz durch Auszählen der Schwingzeit T [sec] bestimmt werden, die benötigt wird, um n-mal dieselbe Schwingungsgrenzlage zu erreichen. Die Schwingungsfrequenz f ergibt sich dann zu: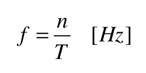 
Man beachte, dass man beim Drücken der Stoppuhr beim Erreichen dere Start-Schwingungsgrenzlage mit der Zahl Null zu zählen beginnt, da sonst eine Schwingung fehlt. Durch Einsatz eines Theodolithen oder Nivelliergerätes lassen sich (bei kleinen Frequenzen) mit Hilfe eines am schwingenden Objekt angeklemmten Maßstabes Grenzwerte der Schwingungen ablesen. Weitergehende Auswertungen, also z.B. Bestimmung der Phasenlage und der Schwingungsformen, sind so i. Allg. nicht möglich, dennoch wird diese Vorgehensweise häufig für eine erste Beurteilung ausreichen. Eine interessante Perspektive ergibt sich heute durch den Einsatz von heute vielfach vorhandenen Videokameras. Videoaufnahmen können heute auch mit fast jedem Smartphone gemacht werden. Da die Video-Recorder oder entsprechende Programme heute durchweg die Möglichkeit bieten, Standbilder zu zeigen, kann die Videoaufnahme angehalten werden und das Objekt am Bildschirm ausgemessen werden. Hiermit lassen sich, neben dem Auszählen der Schwingzeit am Bildschirm, auch maximale Verformungen festhalten und darüber hinaus auch Schwingungsformen bestimmen. Durch Ausmessen der Reduktion der Schwingungsamplituden einer freien Schwingung lassen sich zusätzlich Anhaltswerte über die Dämpfung ermitteln. Wichtig ist hierbei, ebenso wie bei der Messung mit Theodolith, dass die Messung senkrecht zur Schwingungsebene erfolgt. Insbesondere bei verti-kalen Kragträgern treten oft ovalisierenden Schwingungen auf, hier interessiert i. Allg. der größte Schwingungs-Halbmesser. Voraussetzung für den Einsatz einer Videokamera ist naturgemäß eine hinreichend große Schwingamplitude. Gegebenenfalls kann man darüber nachdenken, ob nicht mehrere Videokameras, z.B. mit Zoom-Objektiven, eingesetzt werden. Um die Messungen später vergleichen zu können, muss allerdings eine Zeitsynchronisation durchgeführt werden. Diese kann z.B. mit Hilfe eines akustischen Signals (z.B. Klatschen) erfolgen, das von allen Videokameras mit aufgezeichnet wird. Selbstverständlich muss dabei die gfl. unterschiedliche Laufdauer des Schallsignals zu den Videokameras berücksichtigt werden. Vorab sollte geprüft werden, ob durch speziell angebrachte, klar erkennbare Marken (ohne Farbverlauf bei der Wiedergabe) die Ablesegenauigkeit erhöht werden kann. Ein Nachteil bei der beschriebenen Vorgehensweise liegt darin, dass keine unmittelbaren Informationen über den Zeitverlauf der Schwingwege vorliegen. Wenn der Zeitverlauf von Interesse ist, kann zunächst sehr einfach mit Hilfe mechanischer Wegmessung über handgeführten Taster gemessen werden (Ascania-Schwingwegtaster). Der Taster enthält einen Taststift, der mit Hilfe einer Feder an die Messstelle gedrückt wird. Die Bewegungen des Taststiftes werden auf ein durchlaufendes Registrierpapier aufgezeichnet. Obwohl derartige Taster heute noch (gelegentlich) eingesetzt werden, haben sie doch den Nachteil, dass weitergehende Auswertungen sehr mühevoll sind, da die Messergebnisse nicht in Form von analogen Messschrieben oder in digitaler Form für weitere automatisierte Auswertungen vorliegen.
Heute sind auch Geräte auf Laserbasis verfügbar, mit deren Hilfe Wege berührungslos gemessen werden können. Beim Laser-Tracking-Verfahren wird ein Laserstrahl so nachgeregelt, dass er stets einer am schwingenden Objekt befestigten Marke folgt. Die Winkeländerungen werden gemessen. Die Regelzeiten sind hierbei so schnell, dass Wege über größere Entfernungen (ca. 200m) bei üblichen Bauwerkfrequenzen problemlos bestimmt werden können. Die Genauigkeit liegt zur Zeit etwa bei 1cm auf 100m. Die größte Entfernung liegt bei immerhin 15000m !
Wenn die Messung der absoluten Messgröße gegen einen Festpunkt nicht möglich ist, muss relativ gemessen werden. Hierzu werden heute durchweg elektro- mechanische Geber eingesetzt, so dass eine entsprechende Messausrüstung erforderlich wird. Die zur Messung der Schwingbewegung eingesetzten Aufnehmer sind, mechanisch gesehen, gedämpfte Einmassenschwinger, die in einem gekapselten Gehäuse installiert sind, welches am Bauwerk befestigt wird. Die Relativbewegung zwischen Aufnehmermasse und Gehäuse, bzw. die Federkraft ist die Messgröße des Aufnehmers. Im foilgenden Bild sind die Messprinzipien dargestellt:
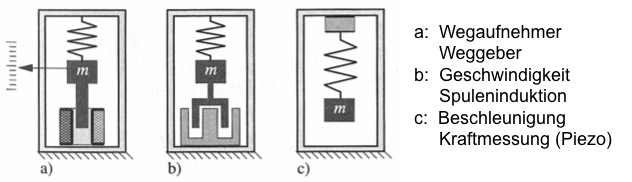
Da der Aufnehmer selbst ein schwingungsfähiges Gebilde darstellt, muss die Schwingungscharakteristik (Übertragungsfunktion) des Aufnehmers bekannt sein, wenn das Messsignal richtig interpretiert werden soll. Ein Aufnehmer, der in Resonanz gerät, wird keine hinreichend genaue Messung der Bauwerksschwingung zulassen.
Die modernen Smartphones haben heute in der Regel Beschleunigungsaufnehmer installiert, die von speziellen Apps ausgelesen werden können. In der Regel haben diese Apps auch eine kleine SIgnalverarbeitung mit „an Bord“, so dass z.B. rasch eine Frequenzbereichstransformation gemacht werden kann. hIeraus kann man die Eigenfrequenzen des schwingenden Systems direkt ablesen.
Bilder eines smartphone-Messschriebes, Zeit undFrequenz..
Die Aufnehmer messen die entsprechenden Messgrößen am Ort der Anbringung. Eine Anbringung z.B. am Geländer eines Bauwerkes (aus Gründen der Bequemlichkeit) misst deshalb auch die i. Allg. nicht interessierende Geländerschwingungen mit und nicht nur die eigentlich interessierende Messgröße des Bauwerkes. Die Anschlusskabel müssen abgeschirmt sein. Alle Abschirmungen, sowie die Masse der Messgeräte, dürfen nur an einer Stelle geerdet werden, um Kriechströme zu vermeiden. Die Anschlusskabel speziell der Beschleunigungsaufnehmer sollten in der Nähe der Aufnehmer mit Hilfe von Klebeband o.ä. befestigt werden, sie dürfen nicht frei aus dem Aufnehmergehäuse heraustreten, da sonst die Kabelschwingungen vom Aufnehmer gespürt werden, das eigentliche Nutzsignal wird verrauscht.
Für jede Schwingungsuntersuchung wird eine Erregung des Systems erforderlich. Häufig werden dazu die natürlichen oder planmäßigen Einwirkungen verwendet, wie z.B. Wind auf ein Bauwerk oder Verkehr auf einer Brücke. Da diese Erregungen zufällig sind, spricht man auch von stochastischen oder Zufallserregungen. Um statistisch gesicherte Ergebnisse zu erhalten, sind ausreichend lange Messdauern erforderlich (bei Windeinwirkung z.B. 1 Stunde und länger). Die so erhaltenen Zeitschriebe können anschließend ausgewertet werden [2,3], man erhält z.B. Eigenfrequenzen, Dämpfungen und Schätzungen der spektralen Antwortleistungsdichte. Bei Aufbringung einer definierten Beanspruchung spricht man von einer determinierten Erregung des Systems. Diese kann entweder transient (abklingend) oder stationär sein.
Stationäre harmonische Erregung am Bauwerk – zum Zwecke der Messung des dynamischen Verhaltens – wird üblicherweise mit Hilfe von Unwucht-Erregern vorgenommen. Hierbei werden die harmonischen Wechselkräfte rotierender Unwuchten ausgenutzt. Durch Anbringen von zwei gegenläufigen Unwuchten kann man die Richtung der Wechselkraft festlegen, siehe folgendes Bild. Im Teil a des Bildes ist nur eine Masse vorhanden, diese erzeugt eine Unwuchtkraft, deren Resultierende in Richtung der Unwucht verläuft, es gibt also stets zwei Komponenten am Auflager. Wenn zwei gleich große Massen gegenläufig installiert werden, heben sich die Massenkräfte in der einen Richtung auf, in der anderen Richtung verstärken sie sich, Bild Teil b und c.
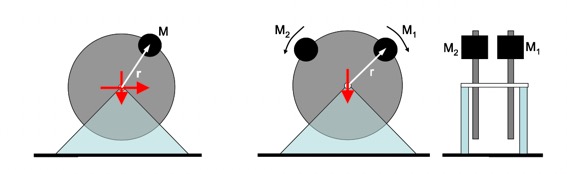
Bei nur einer umlaufenden Masse tritt die Kraftwirkung immer in Richtung des Vektors Drehachse-Masse auf, es gibt also an der Achse immer zwei Komonenten, die die Erreger absetzt. Wenn zwei gegenläufige Massen eingesetzt werden, verstärken sie ihre Wirkung, wenn die Massen gleichgerichtet wirken, wirken sie 90° weiter gegen einander, hben sich die Massenkräfte auf. Bei 180° Phasenverschiebung wirken die Massen wiederin eine Richtung aber entgegengesetzt zur Richtung 0°. Im folgenden Bild ist eine Realisierung gezeigt:
Hierin ist m_u die umlaufende Unwucht-Masse, r der Radius von der Drehachse bis zum Schwerpunkt der Masse und Ω die Kreisfrequenz der Rotation.
Die auftretenden Kräfte sind proportional zum Quadrat der Umlauffrequenz. Es gilt: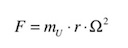 
. Der Verlauf der Kraftwirkung bei der gezeigten Anordnung ist horizontal, d.h. maximale Kraftwirkung, wenn die Massen in gleicher Stellung sind. In der im Foto dargestellten Situation heben sich die Umlenkkräfte beider Massen auf.
Die entstehenden Unwuchtkräfte sind bei niedrigen Frequenzen, bedingt durch das Quadrat der Winkelgeschwindigkeit, sehr klein. Für sehr niedrige Frequenzen, wie bei Bauwerken z.B. gelegentlich 0,1Hz d.h. Omega=2xpix0,1 etwa 0.6 [1/s] werden sehr große Massen benötigt, um eine ausreichende Kraftwirkung zu erzeugen.
Der Vorteil einer stationären Erregung liegt in der Tatsache, dass die vorhandene Energie auf eine Frequenz konzentriert ist, damit ist das Nutz- zu Rauschsignal Verhältnis groß. Da die Übertragungsfunktion direkt gemessen werden kann, können auch frequenzabhängige Dämpfungen einfach ermittelt werden. Der Aufwand ist allerdings beträchtlich. Zur Erregung tieferer Bauwerkseigenfrequenzen sind sehr große Massen erforderlich. Die Drehzahlregelung muss so fein sein, dass Frequenzen in [Hz] mit mindestens zwei Nachkommastellen eingestellt werden können, um die zum Teil sehr schlanken Resonanzspitzen ausmessen zu können. Darüber hinaus muss jeweils der eingeschwungene Zustand abgewartet werden, bevor gemessen werden kann, was eine langdauernde Versuchszeit bedeutet. Wenn die Unwuchtmaschine in Resonanz erregt kann es manchmal schwierig werden, durch Erhöhung dere Motordrehzahl wieder aus der Resonanz heraus zu kommen. Die Unwuchtmaschine tut sich schwer, diesen Bereich zu verlassen und man braucht oft große Energien um sie dazu zu zwingen. Die Nutzung z.B. transienter Erregung ist in der Regel einfacher.
Erregung mit Gleitsinus
Gelegentlich werden auch Sinusfunktionen mit ansteigender Frequenz als Erregung genutzt, im Englischen auch chirp-signal (to chirp=zwitschern) oder sine sweep signal genannt, siehe das Folgebild:
Damit wird bei einem Versuchsdurchgang ein größerer Frequenzbereich überstrichen und die Messungen gehen insgesamt rascher vonstatten. Eine Frequenztransformation des Antwortsignals zeigt dann deutlich die Resonanzspitzen, welche die Eigenfrequenzen des Systems darstellen. Die Erzeugung eines sauberen Chirp-Signals setzt natürlich eine gute Regelung und einen Signalgenerator voraus., ist also aufwendiger als ein konstanter Sinus zu erzeugen.
In den meisten Fällen wird bei Schwingungsmessungen wegen des geringeren Aufwandes eine transiente Erregung vorwendet. Je nach Größe des Messobjektes und Lage der Eigenfrequenzen eignen sich hierfür verschiedene Vorgehensweisen. Zunächst mache man sich bewusst, dass kurze Zeitsignale stets eine breitbandige Frequenzantwort bewirken und umgekehrt. Es werden sehr viele harmonische Einzelschwingungen benötigt, um das kurze Zeitsignal abzubilden. Ein kurzer Last-Zeitprozess hat demnach ein breites Frequenzspektrum, ein langdauernder Last- Zeitprozess ein schmales Frequenzspektrum.
Im fiolgenden Bild ist für verschieden lange Impulsdauern das zugehörige Frequenzspektrum abgebildet:
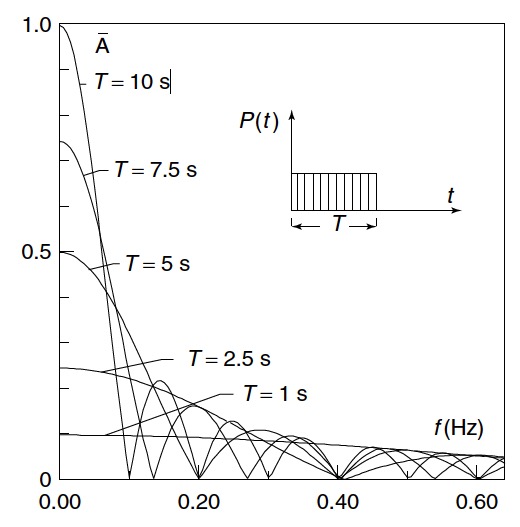
Man erkennt, dass lange Impulsdauern T zu hohen Frequenzen im niederfrequenten Bereich führen, es werden also große Energien im niederfrequenten Bereich abgegeben. Dies ist z.B. der Effekt, der durch das sog. Anzupfen von Bauwerken genutzt wird. Das Bauwerk wird z.B. mit einem Seil horizontal verformt, dann wird das Seil gekappt. Die Impulsdauer ist sehr groß, die Energie wird überwiegend bei niedrigen Frequenzen umgesetzt.
Bei kleineren Objekten wird die transiente Erregung häufig mit einen Hammerschlag auf das Objekt erzeugt. Der Kraft-Zeitverlauf kann über einen Spitzendruckaufnehmer gemessen werden. Es gibt sog. Impulshämmer zu kaufen, die einen Druck-oder Kraftaufnehmer integriert haben, siehe Bild:
Da ein kurzer Hammerschlag ein hochfrequentes Spektrum aufweist, bei dem niederfrequente Anteile nur mit geringer Energie vorhanden sind, eignet sich die Methode schlecht zur Anregung von niedrigeren Grundschwingungen. Das Verhalten kann verbessert werden, indem der Hammer eine Gummikappe erhält, was den Impuls zeitlich verlängert und damit das Spektrum in den niederfrequenten Bereich verschiebt. Anregungen mit einem Hammer werden in der Praxis nur für Schwingungsuntersuchungen von Einzelbauteilen oder sehr kleinen Strukturen angewendet. Größere Bauwerke werden dagegen – wie oben beschrieben – häufig angezupft, indem ein Seil bis zu einer definierten Vorspannkraft gespannt und anschließend gekappt wird. Ein derartiger Entlastungssprung hat einen sehr großen niederfrequenten Frequenzanteil, weshalb er für Bauwerke mit niedrigen Eigenfrequenzen ideal ist [2,3]., vgl. auch den „Anzupf“versuch im Abschnitt Messen. Als „Widerlager“ für das gespannte Seil wurde ein kiesbeladener LKW verwendet, an dem das Zugseil befestigt war, Das Zugseil wurde mit einem Seilzug vorgespannt und dann mit einem Bolzenschneider durchtrennt. Das Durchtrennen führt wahrscheinlich zu keinem abrupten Abfall der Seilkraft ám oberen Seilanknüpfungspunkt am Mast, da nicht alle Einzeldrähte gleichzeitig freiwerden. Außerdem hat das lange Seil auch eine gewisse Masse, die sich dem Rückschnellen des Mastes widersetzt. Hinzu kommt das Schleifen des Seils auf dem Boden. Alles zusammen führt dann zu einer Seilkraftabnahme über einen Zeitraum von vermutlich Millisekunden. Den Masseeffekt des Seils kann man im Modell erfassen, indem eine angekoppelte Masse am Anknüpfungspunkt eingeführt wird. Die beschriebenen Effekte wurden im konkreten Fall als sekundär angesehen und nicht weiter berücksichtigt.
 |
 |
| Mast Heidelstein | Kappen des vorgespannten Seils |
Mit Hilfe eines solchen Anzupfversuches lassen sich viele Informationen sammeln. Über eine theoretische Untersuchung des Lastfalls „Anzupfen“, d.h. aufbringung einer Horizontallast am Seilanknüpfungspunkt, die zum Zeitpunkt des Anzupfens schlagartig auf Null abfällt Aus der Fourier-Transformation der Zeitreihe erhält man das zugehörige Frequenzspektrum, das dierekt mit dem gemessenen verglichen werden kann. Im folgenden BIld ist der Vergleich dargestellt:
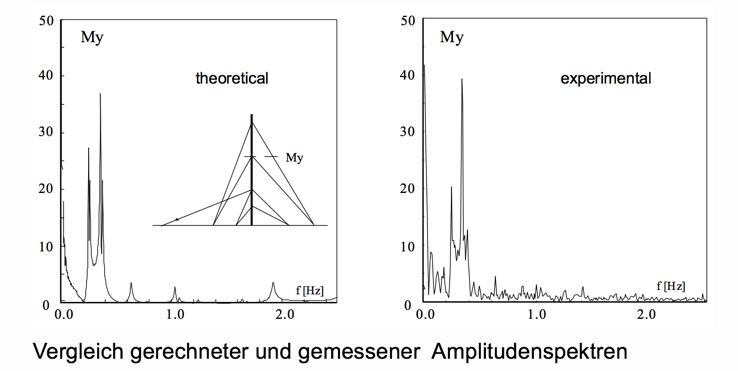
Man erkennt, dass die Verläufe qualitativ recht gut übereinstimmen, die wesentlichen gemessenen Bauwerksfrequenzen werden wiedergegeben. Darüber hinaus enthält das gemessene Signal noch zufälliges Rauschen, was aber hier den Vergleich nicht verhindert. Bei größeren Störungen müsste der hochfrequente Rauschanteil, ggf. über ein Tiefpassfilter vom hochfrequenten Rauschen befreit werden. Solche Programme sind für den Digitalrechner erhältlich.
Sehr viel einfacher wird die Messung, wenn keine spezielle Last aufgebracht werden muss, sondern wenn die ohnehin vorhandenen ambienten Lasten zur Erregung verwendet werden. Ambiente (lat. ambiens = herumgehend, auch umgebend) Lasten sind also Lasten die in der Umwelt vorhandne sind. Z.B. Wind, Welle, Schall und ggf. planmäßiger Verkehr. Brücken tragen die Verkehrslast, die zu Schwingungen im Bauwerk führen, vgl. die untersuchte Eisenbahnbrücke im Folgebild: Links die Situation, rechts den gemessenen Verlauf am Querträger der Brücke. Deutlich erkennt man die großen Lasten der schweren Lok und die Radsätze der Wagen:
 |
 |
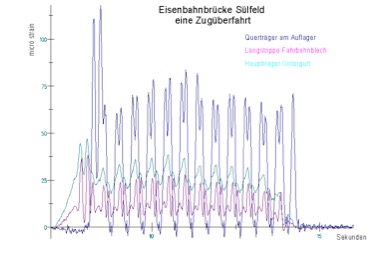| Eisenbahnbrücke Sülfeld | Antwort eines Querträgers |
Ein Problem bei Nutzung der ambienten Last ist, dass diese größenmäßig in der Regel nicht bekannt sind. Dennoch kann man einige nützliche Informationen aus ihnen ziehen. Hierzu sollten wir uns erinnern, dass an einer Resonanzspitze des Frequenzspektrums nur die zugehörige Eigenform signifikant antwortet. Wenn wir weiter voraussetzen, dass am Resonanzpeak nur diese eine Mode antwortet und gleichzeitig die Dämpfung klein ist, wie im Bauwesen allgemein üblich. In diesem Falle gibt es keinen Phasenshift, d.h. das System antwortet phasenrichtig. Dies bedeutet analytisch, dass der imaginäre Anteil der komplexen ANtwort gleich Null ist. In diesem Fall kann die Antwort an 2 Punkten des Systems wie folgt beschrieben werden:
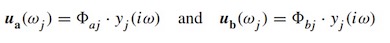
mit
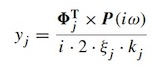
weil die modale Antwort (d.h. die zugehörige Eigenform´)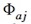 
in der j ten Eigenfrequenz genau der Wert des Eigenvektors j am Punkt a ist. P ist der unbekannte Erregungs-Vektor, 
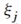ist der Dämpfungswert der j ten Eigenfrequenz und 
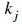ist die modale Steifigkeit nach der folgenden Formel:
.
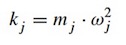Nach Bildung des Verhältnisses:
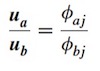
erkennt man, dass die modale Antwort, die die unbekannte Last enthält, durch Kürzung der Last im Zähler und Nenner, unabhängig von P dargestellt werden kann. So können die Komponenten der Eigenmoden an den a=1, 2, 3, …. Freiheitsgraden des Systems betimmt werden. Anschließend sollten sie durch Division des betreffenden Wertes an der Bezugsstelle b dimensionslos gemacht werden.
Die Beziehungen gelten auch, wenn es sich bei den Einwirkungen um stochastische, d.h. Zufallslasten handelt. Hier muss allerdiungs, zur Dämpfungsbestimmung die Leistungsspektraldichte (power-spectral-density (PSD), statt des einfachen Antwortspektrums verwendet werden. DIe PSD muss dazu aus hinreichend langen Messreihen der Antwort bestimmt werden. Informationen hierzu findet man in [13]. Die Resonanzspitzen (peaks) kann man aus dem Antwort-Leistungsspektrum (PSD) entnehmen. Mangels Kenntnis der Belastung können allerdings keine modalen Massen bestimmt werden. Die Dämpfung der Struktur kann aus der Halbwertsbreite der Antworts-Autokorrelationsfunktion bestimmt werden. Auch hierzu sind hinreichend lange Meßreihen erforderlich (>= 1 Stunde bei hinreichend genauer Abtastung). Misst man zu kurz, wird gegen das Gesetz der großen Zahl der Statistik verstoßen und man erhält falsche, d.h. Zufallsergebnisse.
Die Dämpfung kann aber auch anders bestimmt werden [31]:
Wenn ein System durch einen Zufallsprozess mit annähernd konstanten Frequenzverlauf (Weißes Rauschen) im Bereich der interessierenden Eigenfrequenzen erregt wird, ist die Antwort proportional zur mechanischen Leistungsübertragungsfunktion. Wenn durch Rüpcktransformation in den Zeitbereich die Autokorrelationsfunktion bestimmt wird, kann aus deren AMplitudenabfall ebenfalls auf die Dämpfung geschlossen werden,
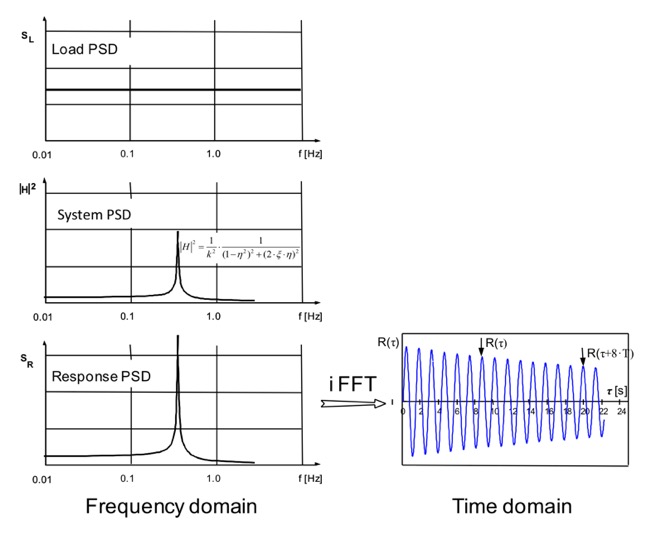
Sie ergibt sich , ganz analog zur Bestimmung des logarithmischen Dekrements, durch den Vergleich der Amplitudenabnahme von zwei aufeinander folgenden Amplituden, Dies ist meist, wegen der geringen Größenunterschiede stark fehlerbehaftet, so dass man in dere Praxis in der Regel eine Reihe von Amplituden auslässt und die Amplitudenabnahme, z.B. nach k=10 Schwingungen ausmisst. Das daraus erhaltene, logarithmische Dekrement ist natürlich zu groß, es muss dann durch die Anzahl der Zwischenschwingungen dividiert werden, es gilt:
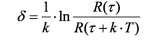
Dabei ist k die Anzahl der Schwingungen (Perioden) von der Bezugsamplitude zur weiter entfernten Amplitude. Im o.a. Beispiel ist z.B. k=8.
[1] Schütz, W. Fatigue life prediction by calculation: Facts and fantasies. Structural Safety & Reliability (Ed. Schueller&Yao). Rotterdam, Baalkema, 1994, 1125-1131.
[2] Peil,U. Assessment of bridges via monitoring. 2005, Structure and Infrastructure Engineering. 2005. 2: 101-117.
[3] Peil, U., Mehdianpour, M., Frenz, M.: Fatigue Prediction of Steel Structures by means of Monitoring and Testing. In: Life Cycle Cost Analysis and Design of Civil Infrastructure Systems. 2001. 222-238.
[4] Dyrbye,C., S.O. Hansen. Wind Loads on Structures. J. Wiley&Sons, NY, 1996.
[5] Peil, U., Frenz, M., Hosser, D., Dehne, M.: Life Time Estimation of Steel Structures and Assessment of critical Details. Proc. Of Int. Conf. Struct. Faults and Repair, London. 2003.
[6] Peil, U.: Life Time Prolongation of Civil Engineering Structures via Monitoring. Proc. 4th Int. Workshop on Struct. Health Monitoring. 2003. 64-78.
[7] Opitz,H., J. Quade, P. Schwesinger, K. Steffens. Das Belastungsfahrzeug BELFA für die Tragsicherheitsbewertung von Massivbrücken und Abwasserkanälen. Bautechnik. 2001.
[8] Belfa – Cooperative research project. www.belfa.de
[9] Peil, U., D. Ruff. Development of Lightweight Girders Made of Sandwich Elements. Proc. 5th Structural Specialty Conference. CSCE. 2006. 83-89.
[10] Box, G.E.P., G.M.Jenkins. Time series analysis. Forecasting and control. Holden Day, San Francisco. 1976.
[11] Link,M., A.Vollan. Identification of Structural System Parameters from Dynamic Response Data. Zeitschrift für Flugwissenschaft und Weltraumforschung, ZFW 2, 1978.
[12] Krätzig, W.B., K. Meskouris, M.Link. Baudynamik und Systemidentifikation. In: Der Ingenieurbau – Baustatik, Baudynamik. Ernst&Sohn, Berlin 1996. 365-517
[13] Jones,N.P., T. Shi, H. Ellis, R.H. Scalan. System-identification procedure for sys-tem and input parameters in ambient vibration surveys. Journ. Wind Eng. Industri-al Aerodynamics. 1995. 91-99.
[14] Ariarathman, S.T., G.I. Schueller, I.Elishakoff. Stochastic structural dynamics. Elsevier. Applied Science Punblishers. 1988.
[15] Keats Wilkie, W. Low-cost piezo-composite actuator for structural control applica-tion. SPIE’s 7th Annual Intern. Symp. On Smart Structures and Materials. 2000.
[16] Heinzmann, A., E.Hennig, B.Kolle, S.Richter, H.Schwotzer, E.Wehrsdorfer. Pro-perties of PZT Multilayer Acctuators. Actuator 2002.
[17] Peil, U.; S. Loppe. An approach for monitoring plane structures with low-cost transducers. Proc. 6th Int. Workshop on Structural Health Monitoring. DEStech Publications, Inc., Lancaster. 2007. 1004-1011.
[19] Abramov,O.V. High intensity ultrasonics. Gordon and Breach Science Publishers. Amsterdam. 1998.
[20] Breitenstein,O., M.Langenkamp. Lock-in thermography. Basics and use for func-tional diagnostics of elevtronic components. Springer-Vlg. Berlin, Heidelbg, New York. 2003.
[21] Andkjær Nielsen, Agerskov H. & Vejrum, T. 1995. „Fatigue damage accumulation in steel bridges under highway random loading“ Proc. 1st European Conf. On Steel Struct. Eurosteel 95. Athens 1995
[22] Moses,F. Weigh-In Motion System Using Instrumented Bridges. Engineering, Proc. ASCE, 1979. Vol105, No.TE3,
[23] Tatsuya,O. BWIM systems using truss bridges. In Ryall,M., G.Parke, J.Harding. (ed), Bridge Management Four, Guildford/Surrey. 2000, 378-385.
[24] Peil,U., M.Mehdianpour. „Life Cycle Prediction via Monitoring“ Proc. 2nd Intern. Workshop on Structural Health Monitoring. DEStech Publications, Inc., Lancaster. 1999 .723-730
[25] Sokolik, A.. Experimental investigation of traffic load on highway bridges. Proc. Conf. IABSE.1993. 85-92
[26] Waubke,H., W.Baumgärtner. Traffic load estimation by long-term strain measure-ments. Proc. Conf. IABSE.1993. 427-434
[27] Deichsel,G., Trampisch,H.J. Clusteranalyse und Diskriminanzanalyse. Gustav Fi-scher Verlag; Stuttgart. 1985.
[28] Drosner, S. Beitrag zur Berechnung der dynamischen Beanspruchung von Brü-cken unter Verkehrslasten. Dissertation, RWTH Aachen. 1989.
[29] Peil,U., M.Mehdianpour, R.Scharff. Life Time Assessment of Existing Bridges. Proc. 2nd Int. Workshop on Struct. Health Monitoring. 2001. 365-383.
[30] Peil, U.: Baudynamik für die Praxis. Stahlbau Kalender 2008, 2008, Hrsg.: U. Kuhlmann, Verlag: Ernst & Sohn
[31] Peil, U.: Civil Infrastructure Load Models for Structural Health Monitoring. In: Encyclopedia of Structural Health Monitoring, Wiley, 2009, p.143-170.
