Wirbelerregte Querschwingungen
2.1 Erregermechanismus
Bei kreisförmigen Querschnitten, also Kaminen, Rohrmantelmasten, Seilen o.ä. lö-sen sich von den gegenüberliegenden Seiten rhythmisch Wirbel ab, es bilden sog. Wirbelstraßen (Bild 2.5a). Wenn sich ein Wirbel auf einer Seite bildet, reduziert sich die Strömungsgeschwindigkeit auf dieser Seite, auf der gegenüberliegenden Seite vergrößert sich die Strömungsgeschwindigkeit (Bild 2.5b). Nach dem Bernoullischen Gesetz folgt hieraus eine im Takte der Wirbelbildung schwankende Druckverteilung, wodurch resultierende Quertriebskräfte entstehen. Wirbelablösungen können auch an kantigen Profilen entstehen, wie Bild 2.6 deutlich macht.
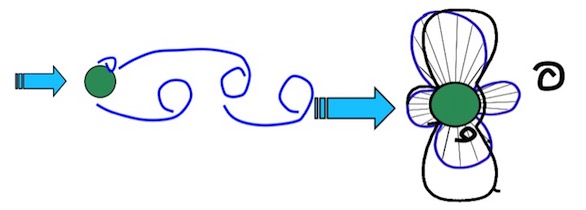

Die Frequenz f der Wirbelablösung ist proportional zur Windgeschwindigkeit und umgekehrt proportional zum Durchmesser, es gilt:
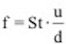
Hierin ist u die Windgeschwindigkeit in m/s und d der Zylinderdurchmesser in m. St ist die sog. Strouhalzahl. Sie ist querschnittsabhängig und in den Normen gegeben. Bei Kreisquerschnitten beträgt sie etwa St = 0,2. Wenn die Ablösefrequenz f mit der Bauwerkseigenfrequenz übereinstimmt, wird das Bauwerk durch die Quertriebskräfte in Resonanz erregt. Die zugehörige sog. kritische Windgeschwindigkeit ukrit ergibt sich aus der o.a. Gleichung durch Einsetzen der Bauwerkseigenfrequenz fi für f. Für die Strouhalzahl St=0,2 ergibt sich:
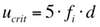 .
.
Trotz der relativ kleinen Quertriebskräfte können bei schwach gedämpften Bauwerken im Resonanzfall sehr große Antworten auftreten. Dies wird deutlich aus dem dynamischen Vergrößerungsfaktor des (generalisierten) Einmassenschwingers unter harmonischer Belastung. Die Vergrößerungsfaktor V der Verformungen infolge der Resonanzerregung gegenüber den Verformungen unter der als statisch wirkend angenommenen Quertriebskraft beträgt:
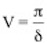
vgl. Grundlagen.
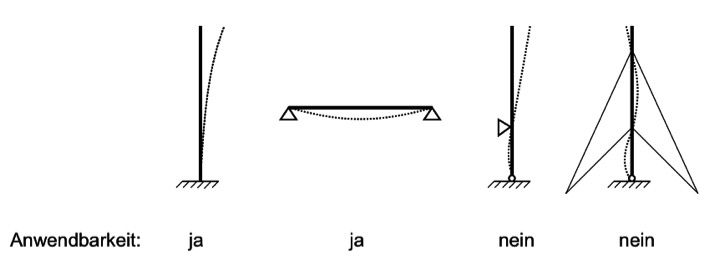
Stählerne, frei auskragende, zylindrische Bauwerke haben i.a. logarithmische Dämp-fungsdekremente δ im Bereich von 0.01 bis 0.03. Der dynamische Vergrößerungsfak-tor liegt dann zwischen ca. 314 und 105, so dass auch sehr kleine Erregerkräfte gro-ße Verformungen und Schnittkräfte hervorrufen. Bei frei auskragenden zylindrischen Bauwerken, wie Kaminen o.ä., stellt dieser Lastfall i.a. den Bemessungsfall dar (Er-müdungsnachweis unter Wechselbelastung). Seilabgespannte Bauwerke zeigen ein wesentlich günstigeres Verhalten als frei auskragende Konstruktionen, insbesondere wenn sie nur gering vorgespannt sind, so dass nennenswerte Seildurchhänge vor-handen sind. Die Ursache liegt in der sich während der Schwingung ständig ändern-den Steifigkeit der Abspannung, das Tragwerk „verstimmt“ sich kontinuierlich in be-zug auf die Erregerfrequenz, es handelt sich um eine nichtlineare Schwingung. Dies führt zu einer wesentlich erhöhten äquivalenten Strukturdämpfung. Bei Querschnitten mit kreisförmigem Querschnitt wird die resultierende Quertriebslast stark vom Strömungszustand in der sehr dünnen Strömungsgrenzschicht, die sich zwischen der Außenströmung und der Körperoberfläche ausbildet, gesteuert. Der Strömungszustand ist von der sog. Reynoldszahl Re abhängig, diese ist wie folgt definiert:
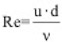
Hierin ist d der Zylinderdurchmesser, u die Anströmgeschwindigkeit und ν = 15⋅10-6 in m²/s die sog. kinematische Zähigkeit der Luft.
Bei Reynoldszahlen Re < 3,5⋅105 bildet sich in der Grenzschicht ein laminarer Strömungszustand aus (unterkritischer Bereich), die Quertriebskräfte werden groß.
Bei größeren als der genannten Reynoldszahl erfolgt vor der Ablösung der Umschlag vom laminaren in den turbulenten Strömungszustand. Der Widerstand fällt schlagartig ab und es bildet sich zunächst eine ungeordnete Nachlaufströmung mit unregelmäßigen Wirbeln aus (überkritischer Bereich). Die Korrelation der lateralen Drücke ist gering, die Quertriebskräfte sinken stark ab.
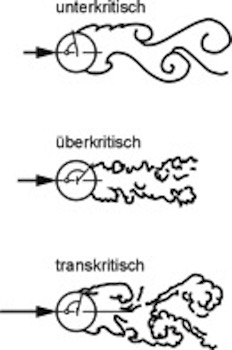
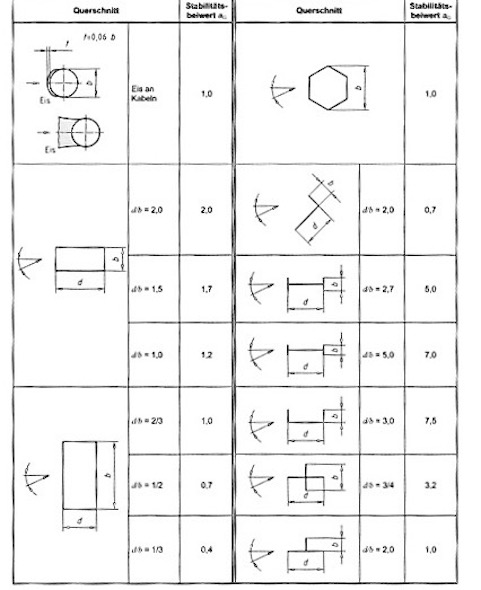
Bei Reynoldszahlen Re > 7⋅10^6 verbreitert sich das Nachlaufgebiet, die ablösende Strömung bildet erneut periodische Wirbel, die Quertriebskräfte wachsen wieder an (transkritischer Bereich). Die Strömungszustände sind im Folgebild schematisch dargestellt. Sie werden von der Rauhigkeit der Zylinderoberfläche erheblich beeinflusst, in geringerem Umfang auch vom Turbulenzgrad der Anströmung. Beide Einflüsse wirken im Sinne einer Erhöhung der Reynoldszahl. Die Strouhalzahl hängt im Wesentlichen von der Querschnittsform ab. In Tabelle 2.2 ist die Abhängigkeit dargestellt. Für scharfkantige Rechteckprofile ergibt sich die Strouhalzahl nach Bild 2.8.
In dem folgenden Diagramm ist die Abhängigkeit der Strouhalzahl bei kantigen Profilen dargestellt:
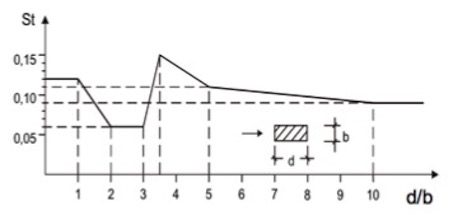
2.2 Ermittlung der Beanspruchungen
Die Größe der Quertriebskraft pro Meter Länge ergibt sich durch Multiplikation des Staudruckes q = u²·ρ/2 in kN/m2 mit dem dimensionslosen Quertriebsbeiwert clat,0 – auch aerodynamischer Erregerkraftbeiwert genannt – und dem Zylinderdurchmesser d. Die Größe des Quertriebsbeiwertes clat,0 kann für kreisförmige Querschnitte in Abhängigkeit von der Reynoldszahl – d.h. vom Strömungszustand (siehe Bild oben) – entnommen werden, vgl. DIN 1055-4, für scharfkantige Querschnitte ist er in der folgenden Tabelle angegeben. Man erkennt, dass der Quertriebsbeiwert bei scharfkantigen Profilen von der Reynoldszahl Re weitgehend unabhängig ist. Wegen der stochastischen Quertriebs-kräfte im über- und transkritischen Bereich hat der Beiwert clat,0 den Charakter eines Effektivwertes.
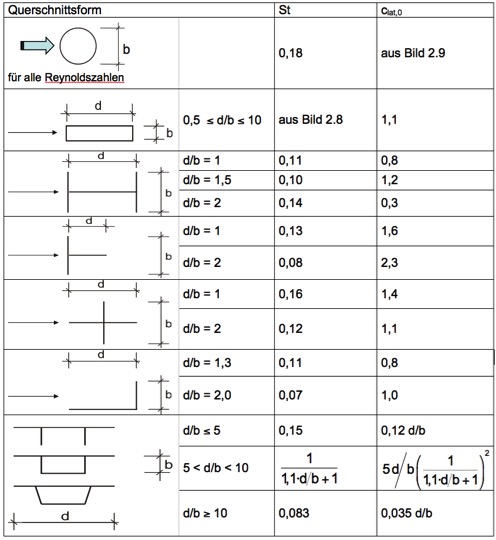
Das folgnde Bild zeigt den Verlauf des sog. Quertriebsbeiwertes über der Reynoldszahl:
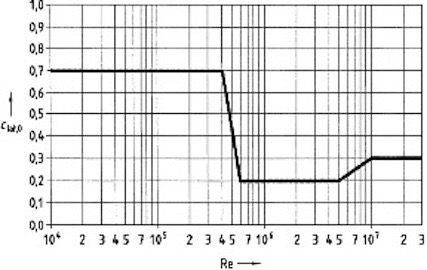
Bei großer Breite des Bauwerks, großer Eigenfrequenz oder kleiner Strouhalzahl ist die kritische Windgeschwindigkeit u_crit groß. Wenn sie deutlich größer ist als die am Aufstellort tatsächlich zu erwartende, so kann es nicht zur Wirbelresonanz kommen. In DIN 1055-4 wird der Abstand mit u_crit > 1,25 um geregelt. Dabei ist u_m die mittlere Windgeschwindigkeit, die pro Jahr mit einer Wahrscheinlichkeit von 0,02 überschritten wird. Ist ukrit = um, so stellt sich die volle Wirbelresonanz noch nicht ein. Ursache sind die turbulenten Schwankungen der Windgeschwindigkeit, die sich der mittleren Geschwindigkeit überlagern, so dass Zustände mit und ohne Resonanz abwechseln. Erst wenn ukrit < um, kommt es zur vollen Resonanzwirkung. Zur Erfassung dieses Effektes wird in DIN 1055-4 (2005-03), Abschnitt D.2.5, der Quertriebsbeiwert reduziert, wenn die kritische Windgeschwindigkeit größer ist als 83% der mittleren Windge-schwindigkeit. Oberhalb vom 1,25fachen der kritischen Windgeschwindigkeit wird der Quertriebsbeiwert zu Null gesetzt. Dazwischen wird interpoliert. Infolge der quasiharmonisch, lateral schwankenden Quertriebskraft werden Schwingungen in schlanken Strukturen erzwungen. Die wesentlichen Beanspruchungen resultieren dabei nicht aus den relativ kleinen Quertriebskräften, sondern aus den Massenkräften der schwingenden Struktur. Der in der o.a. Gleichung angegebene dynamische Vergrößerungsfaktor für einen Einmassenschwinger macht dies deutlich. Die in einem Punkt j entstehenden maximalen lateralen Kräfte ergeben sich dabei durch zweifache Ableitung der harmonischen Schwingwege in lateraler Richtung y:
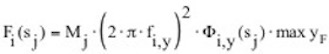
mit
| Mj | die schwingende Masse im Punkt s = sj |
| fi,y | die Eigenfrequenz der i-ten Schwingungsform quer zur Windrichtung |
| Φi,y(sj) | die normierte Schwingungsform i quer zur Windrichtung als Verhältnis |
| der Schwingwegamplitude y im Punkt s = sj zur größten Schwingwegamplitude max yF | |
| max yF | die größte Schwingwegamplitude nach Gleichung |
| s | die Laufkoordinate über die Struktur. Für sich vorwiegend vertikal erstreckende Bauwerke gilt s = z |
Die Berechnung des infolge der Kraft Fi schwingenden Systems wird am einfachsten mit Hilfe der modalen Analyse durchgeführt, bei dem das schwingende System durch eine gewichtete Summe seiner Eigenschwingformen abgebildet wird. Das tatsächliche System wird hierbei in jeder Eigenform durch einen äquivalenten Einmassenschwinger ersetzt, der gleiche Eigenfrequenz und die gleiche kinetische Energie aufweist, wie das in der Eiugenform schwingende tatsächliche System. Hierzu müssen die verteilten Massen und die am System angreifenden, zeitabhängigen Kräfte in äquivalente Massen bzw. Kräfte umgerechnet werden. Bei einem in Resonanz schwingenden System ist immer nur eine zugehörige Eigenschwingform beteiligt, so dass die Berechnung auch nur für eine Eigenfrequenz durchgeführt zu werden braucht. Die äquivalente Masse des in einer Eigenform schwingenden Systems ergibt sich zu (Petersen, 1996):
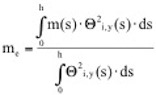
Wenn die Massenverteilung konstant ist, kann sie vor das Integral gezogen werden, die äquivalente Masse entspricht dann der tatsächlichen Massenverteilung. Die äquivalente Erregerkraft ermittelt sich aus der verteilt angreifenden lateralen Luftkraft flat zu:
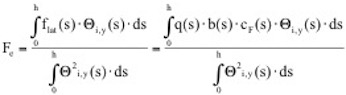
mit q(s) als Geschwindigkeitsdruck bei der kritischen Windgeschwindigkeit, b(s) als maßgebender Breite des Querschnittes und cF(s) als Quertriebsbeiwert. Die maximale Quer-Schwingwegamplitude im Resonanzfall folgt damit zu (vgl. die Vergrößerungsfunktion, oben):
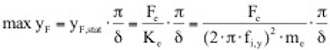
Hierin ist δ das logarithmische Dämpfungsdekrement, fi,y die Eigenfrequenz der i-ten Schwingungsform quer zur Windrichtung. Ke ist die äquivalente Steifigkeit der Feder des äquivalenten Einmassenschwingers, sie ist gleich der Kreisfrequenz ωi = 2πfi,y multipliziert mit der äquivalenten Masse. Wenn in Gleichung für die maximale SChwingweg-Amplitude die äquivalenten Massen und Erregerkräfte eingesetzt wer-den und die absoluten Größen auf Bezugswerte bezogen werden, folgt:
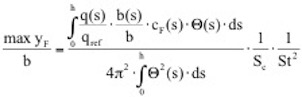
Hierin ist Sc die sog. Scrutonzahl (gelegentlich auch als Massendämpfungsparame-ter bezeichnet), sie ist definiert zu:
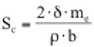
mit ρ als Luftdichte (ρ=1,25kg/m³). Messungen zeigen, dass die Wirbelablösungen in Raum und Zeit fluktuieren. Die maximalen Querlasten treten entlang der Struktur nicht gleichzeitig auf, das führt zur Abnahme der Korrelation siehe Bild 2.10. Die mit wachsendem Abstand von der ma-ximalen Schwingamplitude abnehmende Kreuzkorrelation wird durch die Integration über der Länge L erfasst. L/2 ist hierbei das Integrallängenmaß der Korrelationslänge, d.h. die mittlere Länge der gleichzeitig von Wirbelablösung betroffenen Strukturlänge.
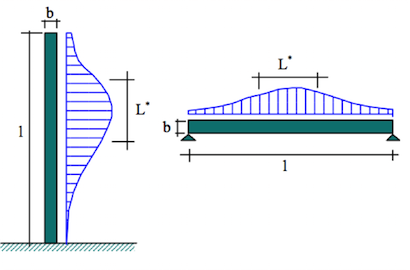
Im Bereich der mittleren Länge der Wirbelablösung, in der die Querlastwirkung per Definition konstant ist, kann für das Integral im Zähler der Gleichung der bezogenen Schwingwegamplitude geschrieben werden:
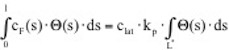
Hierin ist kp der Spitzenfaktor, auch Peakfaktor genannt, vgl. Abs. 2.1, clat ist die Standardabweichung der Querlast. Die maximale Querlast ist also durch die Stan-dardabweichung multipliziert mit dem Peakfaktor ersetzt worden. Der Peakfaktor wird erfasst durch Integration der Schwingungseigenform über der sog. Wirklänge Lj:
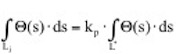
Die Wirklänge erfasst also den Einfluss der Korrelation und den Peakfaktor. Das Ein-setzen der Gleichungen (2.14), (2.15) in Gleichung (2.12) ergibt die maximale Schwingungsamplitude nun wie folgt:
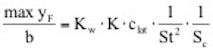
| Dabei ist | ||
|---|---|---|
| b | die maßgebende Breite des Querschnittes im Bereich der Wirbelerregung | |
| Bei zylindrischen Querschnitten ist b der Außendurchmesser | ||
| K_w | der Wirklängenfaktor, siehe Gleichung (2.17) | |
| K | der Beiwert der Schwingungsform, siehe Gleichung 2.18) | |
| clat | der aerodynamische Erregerkraftbeiwert (s. Bild 2.9) | |
| St | die Strouhalzahl nach Tabelle 2.2 und Bild 2.8 | |
| Sc | die Scrutonzahl nach Gleichung (2.13) |
Der Wirklängenfaktor Kw ist wie folgt definiert:
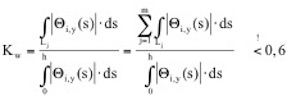
Wenn die untersuchte Eigenform mehrere Maxima aufweist, ist die Wirbelerregung mit der jeweiligen Wirklänge um jedes Maximum herum anzusetzen. In diesem Fall gilt die Summe im zweiten Teil der Formel. In Bild 2.11 sind unterschiedliche Situati-onen mit unterschiedlichen Wirklängenansätzen dargestellt.
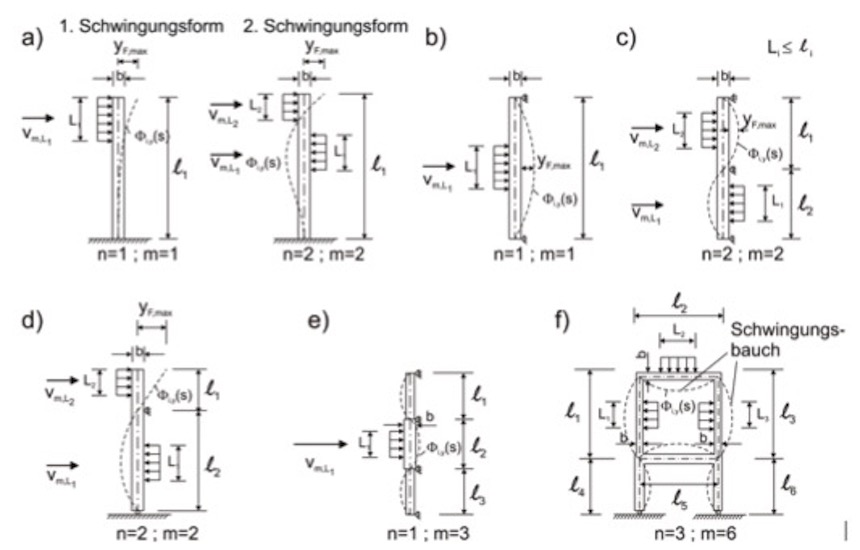
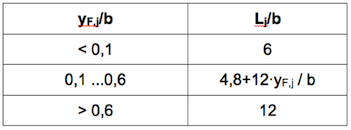
Die Größe der Wirklänge Lj ist in Tabelle 2.3 in Abhängigkeit der Schwingweg-amplitude angegeben. Da die Wirklänge im Bereich der Maxima der Schwingformen anzusetzen ist, entspricht die Schwingwegamplitude i.a. der maximalen Amplitude.
Für einfache Systeme ist DIN 1055-4 (2005-03) der Wirklängenfaktor KW formelmäßig dargestellt, vgl. folgende Tabelle.
Der Beiwert K in Gleichung (2.16) für die Schwingungsform ist definiert zu:
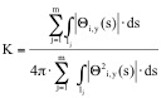
Hierin ist l die gesamte abgewickelte Stablänge. Für einige einfache Strukturen ist der Beiwert zusammen mit den Formeln für den Wirklängenbeiwert in Tabelle 2.4 angegeben.
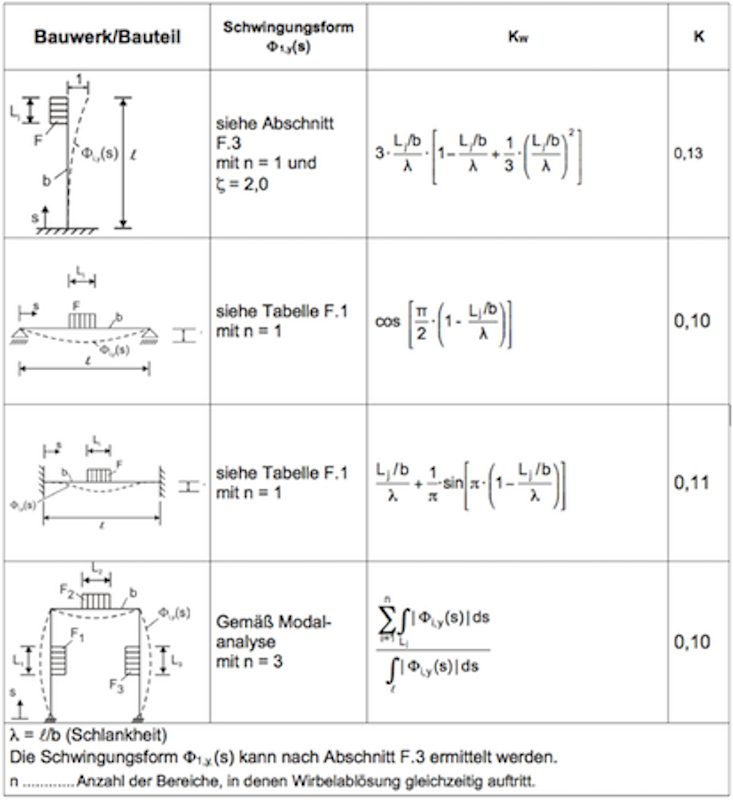
Der Wirklängenfaktor KW ist abhängig von der Schwingwegamplitude y_F,i , vgl. Tabelle 2.4. Die Schwingwegamplitude ist aber wiederum von KW abhängig, vgl. Gleichung (2.16), so dass eine iterative Berechnung erforderlich ist. Es muss zunächst eine Wirklänge Lj angenommen werden, mit der die Schwingwege nach Gleichung (2.16) bestimmt werden. Mit den sich so ergebenden Schwingwegen werden die Wirklän-gen angepasst, bis die Iteration zum Stillstand kommt. Wenn zunächst die maximalen Wirklängen verwendet werden und das Ergebnis auf der sicheren Seite liegt, ist keine weitere Iteration erforderlich. Die ganze Berechnung kann einfach durch ein Tabellenkalkulationsprogramm durchgeführt werden, wenn die Formeln für die Eigenformen unterschiedlicher Systeme mit abgespeichert werden. In DIN 1055-4 (2005-03) sind im Anhang F (Dynamische Grundlagen) Formeln angegeben. Weitere sind der Literatur zu entnehmen, z.B. (Petersen, 1996). Windkanalversuche und Versuche an realen Schornsteinen haben gezeigt, dass das schwingende Bauwerk seine Wirbelstraße in Abhängigkeit von der Schwingamplitude selbst steuert. Es handelt sich deshalb eigentlich nicht um eine Resonanzerregung, wie in den bisherigen Erläuterungen zugrunde gelegt, sondern um eine selbsterregte Schwingung. Dieser Einfluss wird in der Norm durch die Wirklänge erfasst. Die Selbststeuerung der Wirbelstraße führt z.B. bei Erregung in höheren Eigenfrequenzen, wie z.B. bei kreiszylindrischen, abgespannten Masten dazu, dass hier phasenversetzte, d.h. gegensinnige Wirbelablösungen auftreten, die zu einer Art schachbrettartigen Beanspruchung führen, vgl. das folgende Bild. Da sich die Wirbelstraßen bei eng benachbarten, gegenphasigen Erregungen stören, wurde in der DIN 4131 „Abgespannte Antennentragwerke“ festgelegt, dass nur maximal 3 Schwingungsbäuche mit Querbelastung beaufschlagt werden müssen.
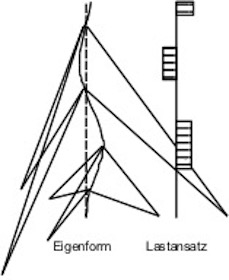
Das geschilderte Verfahren zur Ermittlung der Beanspruchungen ist Grundlage für die Vorgehensweise in DIN 1055-4 (2005-03). Es behandelt die Wirbelerregung wie eine erzwungene Schwingung in Resonanz und erfasst den stochastischen Prozess der fluktuierenden Querlasten durch Ansatz einer geeigneten Wirklänge. Neben die-sem Verfahren der DIN 1055-4 (2005-03) wird im neuen Entwurf des Eurocodes ein weiteres Verfahren angeboten, das auf den Prinzipien des in Abschnitt 2.1 darge-stellten Spektralverfahrens beruht. Dies soll hier kurz dargestellt werden. Infolge der Turbulenz ist die Windgeschwindigkeit nicht konstant, daher schwankt die Ablösefrequenz f in einer gewissen Bandbreite um die Zentralfrequenz : Es entsteht ein Erregerspektrum:
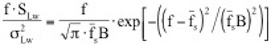
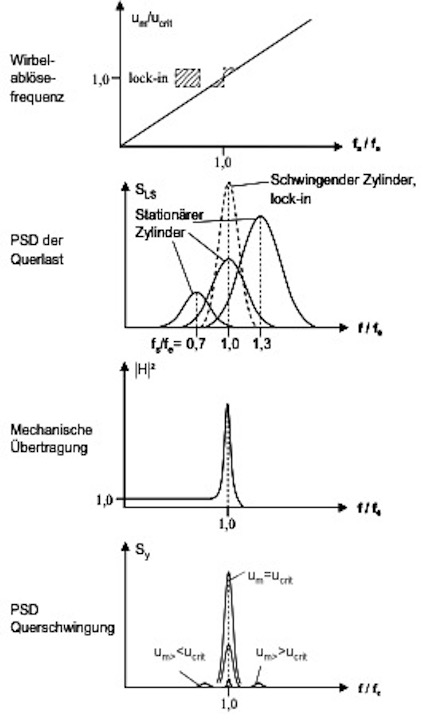
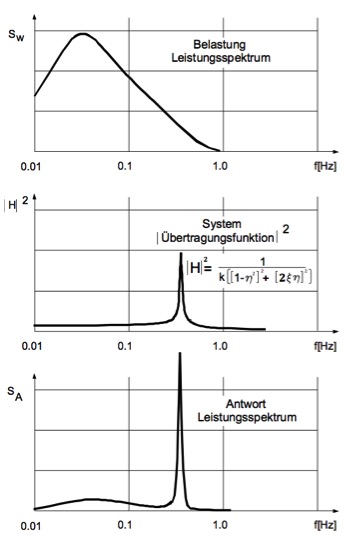
Wie schon bemerkt, steuert bei großen Schwingungsamplituden die Bewegung die Ablösefrequenz in einem bestimmten Geschwindigkeitsbereich. Es kommt zu einem sog. Lock-in-Effekt. Der Vorgang ist in Bild 2.13 illustriert. Die Berechnung der Trag-wergsreaktion folgt dem dort angegebenen Schema, vgl. dazu auch Abs. 2.1. Der Fall der Wirbelresonanz, wenn fsM mit einer Eigenfrequenz fi zusammenfällt, führt zu sehr großen, schmalbandigen Reaktionen. Es ist in der Regel bemessungsmäßig nicht beherrschbar und sollte vermieden werden. Auch außerhalb des Resonanzfal-les kann die Wirbelerregung merkliche, breitbandige Beanspruchungen auslösen.

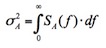
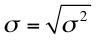 .
. .
.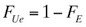 .
.
 .
.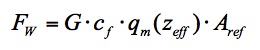 .
.
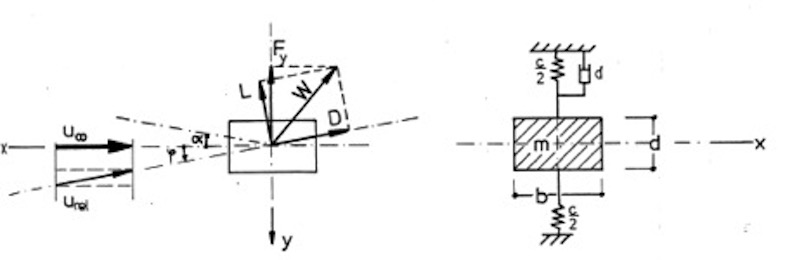
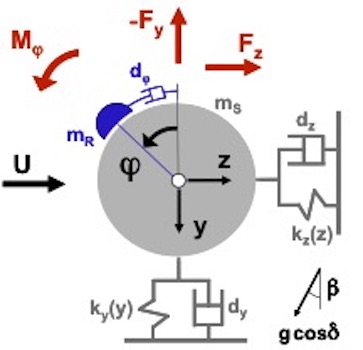
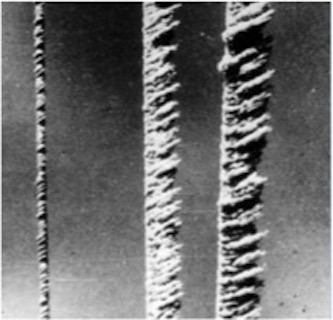
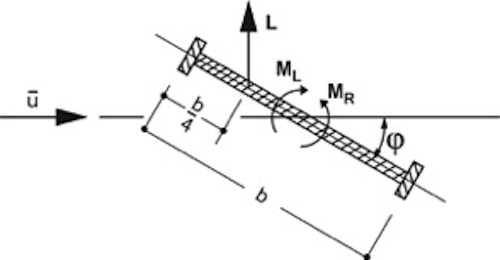
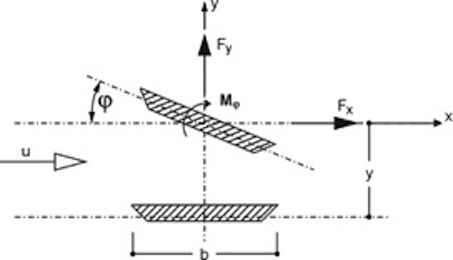
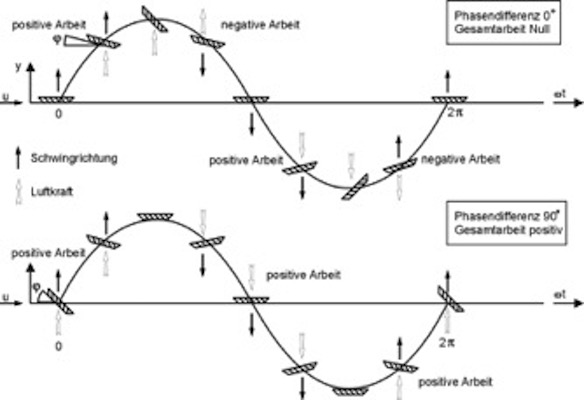
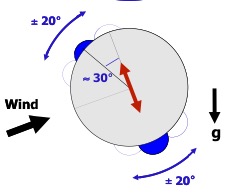
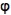 =0) treten zwar auf der Ober- und Unterseite Unterdrücke auf, diese sind jedoch gleichgroß und entgegengesetzt, so dass die resultierende Wirkung auf den Querschnitt gleich Null ist. Wird nun das Profil durch eine Störung in vertikaler Richtung – also senkrecht zur Anströmrichtung – bewegt, ändert die das Profil treffende Windgeschwindigkeit infolge der Vektoraddition mit dem entstehenden „Fahrtwind“ in Querrichtung ihren Einfallswinkel (relativer Wind). Ähnliches bewirkt eine Schräganblasung des Querschnittes unter dem Winkel φ. Es bildet sich eine relative Anströmgeschwindigkeit urel unter dem Winkel
=0) treten zwar auf der Ober- und Unterseite Unterdrücke auf, diese sind jedoch gleichgroß und entgegengesetzt, so dass die resultierende Wirkung auf den Querschnitt gleich Null ist. Wird nun das Profil durch eine Störung in vertikaler Richtung – also senkrecht zur Anströmrichtung – bewegt, ändert die das Profil treffende Windgeschwindigkeit infolge der Vektoraddition mit dem entstehenden „Fahrtwind“ in Querrichtung ihren Einfallswinkel (relativer Wind). Ähnliches bewirkt eine Schräganblasung des Querschnittes unter dem Winkel φ. Es bildet sich eine relative Anströmgeschwindigkeit urel unter dem Winkel 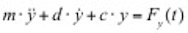
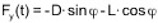
 .
.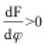
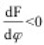 .
.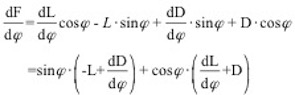
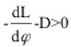 d.h.
d.h. 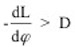 .
.
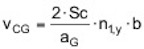
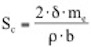
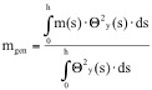
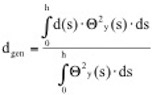
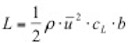
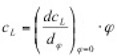
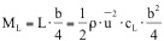
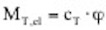 .
.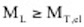 ,
,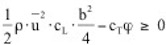
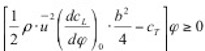
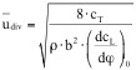
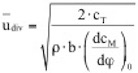
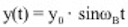
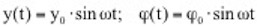 .
.
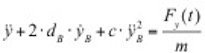
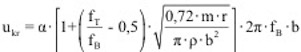
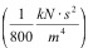
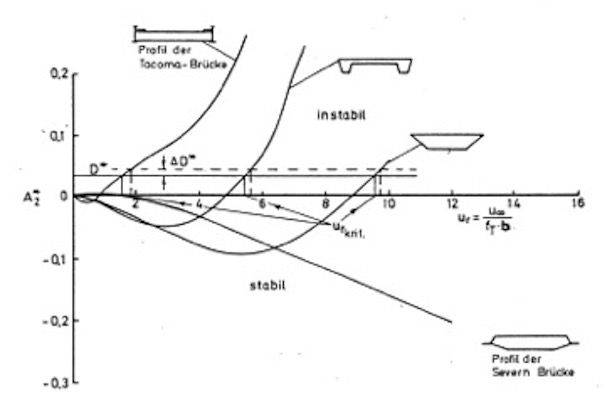
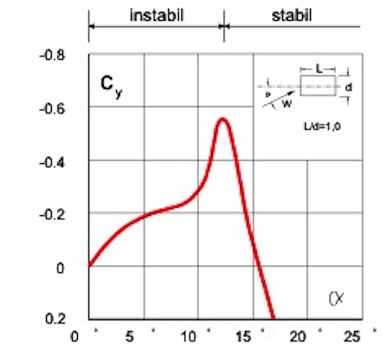
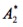 nach Scanlan, eingetragen. Dieser Beiwert wird bei der Lösung der Bewegungsgleichung benötigt und charakterisiert die Torsionsschwingung eines Querschnitts. Analog wird auch der Strukturdämpfungsbeiwert
nach Scanlan, eingetragen. Dieser Beiwert wird bei der Lösung der Bewegungsgleichung benötigt und charakterisiert die Torsionsschwingung eines Querschnitts. Analog wird auch der Strukturdämpfungsbeiwert 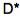 definiert. Schneidet die
definiert. Schneidet die 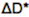 nur ein geringes Ansteigen der kritischen Einsetzgeschwindigkeit zur Folge hat. Man erkennt auch, das die Querschnittsform einen erheblichen Einfluss auf die Einsetzgeschwindigkeit hat. Das Profil der Tacoma-Brücke, die im Jahre 1940 nach spektakulären Flatterschwingungen einstürzte, war offenbar äußerst ungünstig, die kritische Flattergeschwindigkeit wird sehr früh erreicht. Andere Querschnittsformen verhalten sich hier wesentlich günstiger. Optimal ist offenbar der schlanke Querschnitt, wie er bei der Brücke über den Severn (Verbindung Brisol-Cardiff in Groß-Britannien) mit einer Spannweite von 988m erstmalig eingesetzt wurde. Die zugehörige Kurve schneidet die D* nie, der Querschnitt ist absolut flatterstabil. Moderne Brückenentwürfe lehnen sich deshalb an dieses Profil an. Deutliche Abweichungen können aber wieder zu Flattergefahr führen. Eine Erweiterung auf beliebig bewegte Systeme ist in (Starossek, 1992) zu finden. Die Bedingungen für plattenförmige Tragwerke aus dem EC 1991-4 Anhang E4 sind falsch. Untersuchungen an unserem Institut haben gezeigt, dass diese Bedingungen falsch sind, siehe Kirch 2010. Es wird vorgeschlagen die Untersuchungen mit Hilfe des Verfahrens von Klöppel/Thiele 1967 durch zuführen, das relativ einfach ist und eine hinreichend genau Abschätzung der Flattergefahr bringt. Die Flatterwindgeschwindigkeit des aeroelastischen Systems wird dabei mithilfe der potentialtheoretisch beschriebenen Umströmung des dünnen Plattenquerschnitts ermittelt (Lösung in Diagrammen grafisch aufbereitet). Für den real verwendeten Querschnitt wird das Ergebnis pauschal mit einem Faktor modifiziert, der als rein querschnittsabhängig (das ist bei genauerer Betrachtung nicht so) angenommen wird. Die mathematisch angemessene Beschreibung und Untersuchung selbst ebener aeroelastischer Modelle mit nur zwei aerodynamisch wirksamen Freiheitsgraden stellt eine anspruchsvolle Aufgabe dar. Umso wünschenswerter sind einfache Hilfen zur Abschätzung der Stabilitätsgefährdung eines aeroelastischen Systems, wie das Flat-tern beispielsweise einer schlanken Brücke unter Windanströmung. Der Bericht von Kirch 2010 aus unserem Institut beschreibt Untersuchungen zu der Qualität und den Anwendungsgrenzen verschiedener, aus dem Fachschrifttum bekannter Näherungsformeln für die Berechnung der Flatterwindgeschwindigkeit aeroelastischer Systeme. Genauere Algorithmen, die zur Berechnung der Referenzwerte herangezogen wer-den, sind ebenso wie die daraus folgenden Ergebnisse in dem Bericht ausführlich dokumentiert. Mit den erarbeiteten Empfehlungen wird vor allem dem entwerfenden Ingenieur eine Sammlung klarer und nachvollziehbarer Rechenbehelfe an die Hand gegeben.
nur ein geringes Ansteigen der kritischen Einsetzgeschwindigkeit zur Folge hat. Man erkennt auch, das die Querschnittsform einen erheblichen Einfluss auf die Einsetzgeschwindigkeit hat. Das Profil der Tacoma-Brücke, die im Jahre 1940 nach spektakulären Flatterschwingungen einstürzte, war offenbar äußerst ungünstig, die kritische Flattergeschwindigkeit wird sehr früh erreicht. Andere Querschnittsformen verhalten sich hier wesentlich günstiger. Optimal ist offenbar der schlanke Querschnitt, wie er bei der Brücke über den Severn (Verbindung Brisol-Cardiff in Groß-Britannien) mit einer Spannweite von 988m erstmalig eingesetzt wurde. Die zugehörige Kurve schneidet die D* nie, der Querschnitt ist absolut flatterstabil. Moderne Brückenentwürfe lehnen sich deshalb an dieses Profil an. Deutliche Abweichungen können aber wieder zu Flattergefahr führen. Eine Erweiterung auf beliebig bewegte Systeme ist in (Starossek, 1992) zu finden. Die Bedingungen für plattenförmige Tragwerke aus dem EC 1991-4 Anhang E4 sind falsch. Untersuchungen an unserem Institut haben gezeigt, dass diese Bedingungen falsch sind, siehe Kirch 2010. Es wird vorgeschlagen die Untersuchungen mit Hilfe des Verfahrens von Klöppel/Thiele 1967 durch zuführen, das relativ einfach ist und eine hinreichend genau Abschätzung der Flattergefahr bringt. Die Flatterwindgeschwindigkeit des aeroelastischen Systems wird dabei mithilfe der potentialtheoretisch beschriebenen Umströmung des dünnen Plattenquerschnitts ermittelt (Lösung in Diagrammen grafisch aufbereitet). Für den real verwendeten Querschnitt wird das Ergebnis pauschal mit einem Faktor modifiziert, der als rein querschnittsabhängig (das ist bei genauerer Betrachtung nicht so) angenommen wird. Die mathematisch angemessene Beschreibung und Untersuchung selbst ebener aeroelastischer Modelle mit nur zwei aerodynamisch wirksamen Freiheitsgraden stellt eine anspruchsvolle Aufgabe dar. Umso wünschenswerter sind einfache Hilfen zur Abschätzung der Stabilitätsgefährdung eines aeroelastischen Systems, wie das Flat-tern beispielsweise einer schlanken Brücke unter Windanströmung. Der Bericht von Kirch 2010 aus unserem Institut beschreibt Untersuchungen zu der Qualität und den Anwendungsgrenzen verschiedener, aus dem Fachschrifttum bekannter Näherungsformeln für die Berechnung der Flatterwindgeschwindigkeit aeroelastischer Systeme. Genauere Algorithmen, die zur Berechnung der Referenzwerte herangezogen wer-den, sind ebenso wie die daraus folgenden Ergebnisse in dem Bericht ausführlich dokumentiert. Mit den erarbeiteten Empfehlungen wird vor allem dem entwerfenden Ingenieur eine Sammlung klarer und nachvollziehbarer Rechenbehelfe an die Hand gegeben.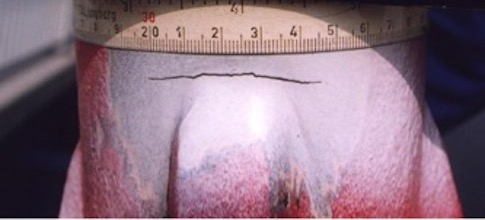
 .
.